Vinkler i sirkler
Aktivitet
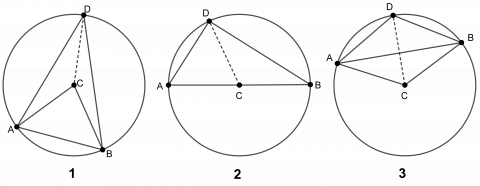
Det er plassert 9 punkter med lik avstand på sirkellinja i figur 1.
Velg to av punktene og kall dem A og B. Kall sentrum i sirkelen C. Tegn trekanten ABC.
Hvor stor er vinkel C?
Velg så et annet punkt på sirkellinja, og kall det D. Tegn trekanten ABD.
Hvor stor er vinkel D?
Hva legger du merke til?
Plasser punktet D i et av de andre punktene på sirkellinja, og lag en ny trekant ABD. Finn på nytt vinkel D.
Hva legger du merke til nå?
Hva skjer hvis du plasserer A OG B i andre punkt på sirkellinja?
Du kan bruke den interaktive figuren nedenfor eller skrive ut ark med sirkler til å tegne på her.
Vil den samme sammenhengen gjelde hvis du plasserer punktene A, B og D på en sirkel uten å bruke oppmerkede punkter med kjent avstand?
Kan du bevise det?
Merk: Vi kaller vinkler med toppunkt i sentrum i en sirkel sentralvinkler, og vinkler som har toppunkt på sirkellinja eller periferien, kaller vi periferivinkler. Vi sier at begge vinklene spenner over buen AB.
Starthjelp
- Hvor stor del av 360˚ er vinkel ACB?
- Figur 2 kan være til hjelp for å finne vinkel D. Hvor store er vinklene i de to trekantene ADC og BDC?
- Det kan være en hjelp i Trekanter i sirkler.
Løsning
Siden sirkelen er delt i 9 like store deler, vil hver sektor ha en sentralvinkel på \(\frac{360^\circ}{9}=40^\circ\), slik figuren viser.
I tilfellet som var tegnet i oppgaven, vil \(\angle ACB = 3\cdot 40^\circ=120^\circ\).
\(\angle ACD = 4\cdot 40^\circ = 160^\circ\). Denne trekanten er likebeint, AC = AD = sirkelradien, så da er vinklene ADC og DAC like store: \(\angle ADC=\angle DAC=\frac{180^ \circ -160^\circ}{2}= 10^\circ\).
Trekanten BCD er også likebeint. \(\angle BCD = 2\cdot 40^\circ=80^\circ\), og \(\angle BDC=\angle DBC=\frac{180^\circ - 80^\circ}{2}=50^\circ\).
\(\angle ADB=\angle ADC+\angle BDC= 10^\circ+50^\circ=60^\circ\).
Vi ser at periferivinkelen ADB er halvparten så stor som sentralvinkelen ACB.
Vi kan tegne opp flere eksempler og regne ut vinkler. Hver gang vil periferivinkelen bli halvparten så stor som sentralvinkelen når vinkelbeina går gjennom de samme to punktene på sirkelbuen.
Vi kan prøve med andre plasseringer av punktene A, B og D. Og vi kan prøve med sirkler som er delt i et annet antall like store deler.
Vi kan tenke oss tre ulike tilfeller:
Vinkel ACB er mindre enn 180˚, vinkel ACB 180˚, og vinkel ACB er større enn 180˚.
Hver gang finner vi at vinkelen med toppunkt på sirkellinja er halvparten så stor som vinkelen med toppunkt i sentrum av sirkelen, når vinkelbeina går gjennom de samme to punktene på sirkelbuen.
Vi påstår at sentralvinkelen er 2 ∙ periferivinkelen når de spenner over samme bue.
Nå har vi vist at dette gjelder for en sirkel som er delt i 9 like store sektorer. Vil det samme gjelde uansett hvor på sirkellinja vi plasserer A, B og D?
Vi påstår at det er tilfellet, men det må vi bevise.
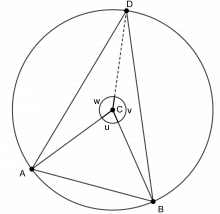
Vi bruker denne figuren:
Det er tre likebeinte trekanter inne i sirkelen, ABC, ADC og BDC, fordi to vinkelbein i hver av trekantene er radier i sirkelen.
\(u = 360^\circ -(v+w)\\ v+w=360^\circ-u\\\angle ADC= \frac {180^\circ -w}{2}\\\angle BDC=\frac {180^\circ -v}{2}\\\angle ADB = \angle ADC+\angle BDC \\ =\frac {180^\circ -w}{2}+\frac {180^\circ -v}{2} \\ =\frac {180^\circ -w+180^\circ -v}{2}\\ =\frac {360^\circ -(v+w)}{2}\\ =\frac {360^\circ -(360^\circ-u)}{2}\\ =\frac{u}{2}\)
Denne sammenhengen vil gjelde i alle tilfeller, så vi har bevist påstanden.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne aktiviteten bygger på Trekanter i sirkler og Sykliske firkanter. Vi introduserer begrepene sentralvinkel, periferivinkel og «å spenne over en bue», men læreren må vurdere hvor mange nye ord det passer å introdusere i klassen.
Elevene vil oppdage at en vinkel med toppunkt i sentrum av en sirkel er dobbelt så stor som en vinkel med toppunkt på sirkelbuen av sirkelen, når begge har vinkelbein som går gjennom de to samme punktene på sirkelbuen. Altså er sentralvinkelen dobbelt så stor som periferivinkelen. Når denne egenskapen er forstått, kan elevene være i stand til å vise at alle periferivinkler som spenner over samme bue, er like store.
Sirkelen i oppgaven er delt i 9 like store deler. Hensikten er at elevene skal kunne konsentrere seg om de geometriske strukturene, uten å bekymre seg om aritmetikken. Et spesialtilfelle er Rette vinkler.
Mulig tilnærming
Elevene kan bruke GeoGebra-appleten i oppgaven, eller de kan få ark å tegne på her.
Ha den interaktive figuren oppe på tavla, og tegn opp eksempler. La elevene samarbeide i par og finne alle vinklene som oppstår når det er tegnet opp linjestykker fra sentrum til alle de tre periferipunktene.
«Vinklene med toppunkt i sentrum blir til sammen 360˚. Hvor store er de tre vinklene ACB, ACD og BCD? Hvordan kan vi finne det ut?»
«Hva slags trekanter er de tre trekantene ACB, ACD og BCD? Hvorfor?»
«Regn ut de øvrige vinklene i de tre trekantene.»
«Er det noen sammenheng mellom vinklene ACB og ADB?»
«Har vi flere tilfeller av sentralvinkler og periferivinkler som spenner over samme bue i figuren? Sammenlign vinklene BCD og BAD. Er det to vinkler som spenner over samme bue? I tilfelle hvilken bue? Finner dere samme sammenheng her? Og hva med vinklene ACD og ABD?»
Utfordre elevene til å overbevise seg om at denne sammenhengen vil gjelde i alle tilfeller, jf. figur 5 under Løsning. Kanskje trenger elevene litt hjelp til «Tilfelle 3», der sentralvinkelen er større enn 180˚.
Eksempel:
I dette tilfellet er a sentralvinkelen og b + c periferivinkelen.
\(a + d + e =360^\circ\\\)
\(a=360^\circ-(d+e)\\\)
\(b=\frac{180^\circ-d}{2}\\\)
\(c=\frac{180^\circ-e}{2}\\\)
\(b+c=\frac{180^\circ-d}{2}+\frac{180^\circ-e}{2}=\frac{180^\circ-d+180^\circ-e}{2}=\frac{360^\circ-(d+e)}{2}= \frac{a}{2} \)
Gode veiledningsspørsmål
- Vi skal sammenligne vinkler med toppunkt i sentrum av en sirkel med vinkler som har toppunkt på sirkellinja (periferien). Hva kan du fra før som kan komme til nytte her?
- Hvilke ekstra navn vil du sette på figuren (på vinkler eller punkter) for å kunne forklare det du ser?
- Kan du formulere det du legger merke til, med egne ord?
- Kan du forklare, og kanskje bevise, det du har lagt merke til?
- Hvilke nye spørsmål kan du stille ut fra det du nå har funnet ut?
Mulig utvidelse
- Vil det du har observert i en nidelt sirkel gjelde, uansett hvor på sirkellinja punktene A, B og D plasseres?
- Kan du bevise det?
Ressursen er utviklet av NRICH