Andregradsfunksjoner IV
Aktivitet
Nullpunkter
I denne aktiviteten trenger du GeoGebra eller et annet digitalt graftegneprogram til flere av oppgavene. Alle grafene skal tegnes digitalt.
Oppgavene kan skrives ut fra dette oppgavearket.
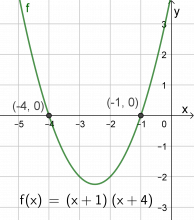
- Tegn grafen til funksjonen \(f(x)=(x+1)(x+4)\). Finn, og noter, nullpunktene til funksjonen.
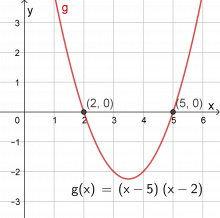
Hvilken form har grafen? hva slags funksjon er f? Hvorfor? - Tegn grafen til \(g(x)=(x-5)(x-2)\). Finn og noter nullpunktene.
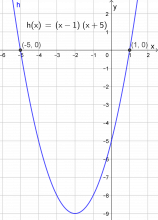
Tegn grafen til \(h(x)=(x-1)(x+5)\). Finn og noter nullpunktene. - Noter, uten å tegne graf, nullpunktene til disse funksjonene. Hvis du er usikker, kan du gjette!
\(\begin{align} j(x)&=(x+3)(x-2)\\ k(x)&=(x-4)(x+6)\\ m(x)&=(x+1)(x-5) \end{align} \) - Tegn grafene til de tre funksjonene j, k og m, og kontroller om det du noterte var riktig. Hvis ikke, kan du se hva som ble feil?
- Lag funksjonsuttrykk til grafer som har følgende nullpunkter:
\(\begin{align} x&=2\text{ og }x=3\\ x&=-4\text{ og }x=8\\ x&=-1\text{ og }x=-2 \end{align}\) - Tegn grafer og kontroller om du løste oppgave 4 riktig. Hvis du gjorde noe feil. kan du se hvorfor det ble feil?
- I funksjonen \(b(x)=(x-7)(x-4)\) er \(x=7\) og \(x=4\) nullpunkter. Hva blir funksjonsverdien når du setter inn \(x=7\) eller \(x=4\) og regner ut?
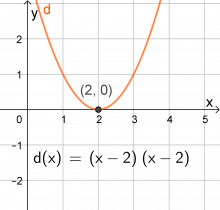
Regn ut verdien av b når \(x=7\) og \(x=4\). Ble det slik som du hadde tenkt? - Tegn grafen til \(d(x)=(x-2)(x-2)\). Finn nullpunktene. Hva ser du? Hvorfor blir det slik?
- Vi sier at funksjoner som for eksempel \(f(x)=(x+1)(x+4)\), er skrevet på faktorisert form, fordi funksjonsuttrykket består av to faktorer (parenteser). Hva er sammenhengen mellom en funksjon på faktorisert form og funksjonens nullpunkter? Skriv med egne ord.
Starthjelp
- Hvordan kan du finne nullpunktene til en funksjon ved å se på grafen?
- Hvordan oppgir vi nullpunkter?
- Til grafen i oppgave 1: Hvilken form har grafen? Hva slags funksjonsuttrykk har slike grafer?
- Hvorfor er en funksjon som \(f(x)=(x+1)(x+4)\) en andregradsfunksjon?
- Hvordan kan du se på en parentes i funksjonsuttrykket om nullpunktet er et positivt eller et negativt tall?
- Hvordan må du tenke når du skal lage faktorer (parenteser) som gir et nullpunkt i en positiv x-verdi? Enn når du skal lage faktor til et nullpunkt med en negativ x-verdi?
- Hva er en faktor?
- Hvorfor sier vi at funksjonsuttrykk som for eksempel \(f(x)=(x+1)(x+4)\) er faktorisert?
Løsning
1.
Funksjonen \(f(x)=(x+1)(x+4) \) har nullpunktene x = -4 og x = -1.
Grafen er en parabel, det er grafen til en andregradsfunksjon. Hvis vi multipliserer ut funksjonsuttrykket får vi et andregradsuttrykk.
2.
Nullpunkter x = 2 og x = 5.
Nullpunkter x = -5 og x = 1.
3.
\(\begin{align} j(x)&=(x+3)(x-2) \text{ har nullpunkter }x=-3 \text{ og }x=2\\ k(x)&=(x-4)(x+6) \text{ har nullpunkter }x=4 \text{ og }x=-6\\ m(x)&=(x+1)(x-5) \text{ har nullpunkter }x=-1 \text{ og }x=5 \end{align} \)
4.
Kontroller i GeoGebra. Løste du oppgave 3 riktig?
5.
En graf med nullpunkter x = 2 og x = 3 er for eksempel \(f(x)=(x-2)(x-3)\)
En graf med nullpunkter x = -4 og x = 8 er for eksempel \(g(x)=(x+4)(x-8)\)
En graf med nullpunkter x = -1 og x = -2 er for eksempel \(h(x)=(x+1)(x+2)\)
6.
Kontroller i GeoGebra. Løste du oppgave 5 riktig?
7.
I funksjonen \(b(x)=(x-7)(x-4) \) er x = 7 og x = 4 nullpunkter.
x = 7 gir \(b(x)=(7-7)(7-4)=0 \cdot3=0\)
x = 4 gir \(b(x)=(4-7)(4-4)=-3 \cdot0=0\)
Nullpunkter er nettopp de x-verdiene som gjør at funksjonsverdien blir 0.
8.
Funksjonen har bare ett nullpunkt, x = 2. Men fordi dette er en andregradsfunksjon, blir grafen en parabel. Parabelen bører x-aksen i bare dette ene punktet.
9.
Når en funksjon er på faktorisert form, inneholder den parenteser som skal multipliseres med hverandre. (Den kan i tillegg inneholde en tallfaktor, men det gjør ingen av funksjonen vi har sett på til nå.) Den x-verdien som gjør en parentes lik 0, vil også gjøre funksjonsuttrykket lik 0. For når 0 er faktor i et multiplikasjonsstykke, blir produktet alltid 0.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
I denne aktiviteten er det søkelys på sammenhengen mellom en funksjons nullpunkter og funksjonsuttrykket på faktorisert form.
Mulig tilnærming
La elevene samarbeide i par.
Aktiviteten er lagt opp slik at elevene skal kunne arbeide seg gjennom alle oppgavene uten at det er behov for stopp og fellessamtaler underveis. De må bruke GeoGebra og de må ha et sted å notere det de kommer fram til. Hvis du ønsker, kan du skrive ut oppgavene på papir. Du finner dem her.
Gjennom arbeidet kommer elevene til å få flere erfaringer med andregradsfunksjoner og grafer. Målet er at de skal se
- at en funksjon som består av et produkt av to førstegradsfaktorer, er en andregradsfunksjon
- at x-verdier som gjør en faktor lik 0, også gjør funksjonen lik 0
- og at disse x-verdiene dermed er nullpunkter for funksjonen
- at du kan finne funksjonens nullpunkter direkte hvis den er på faktorisert form
Følg med på elevens arbeid. Hvis noen trenger det, kan du stille gode veiledningsspørsmål som kan hjelpe dem videre i problemløsningen. Pass på å ikke overta løsningen for dem, men hjelp dem på glid slik at de kan komme videre på egen hånd.
Til slutt må dere ha en felles avslutning og oppsummering. La elevene få presentere løsningene sine, forklare hva de har tenkt og begrunne hvorfor de mener det de har gjort, er riktig. Det er fint om feil og misforståelser kommer fram under oppsummeringen. Vis respekt for feil, det er viktig å få diskutert dem slik at de ikke følger med «på lasset» i det videre arbeidet.
Gode veiledningsspørsmål
- Hvordan kan du finne nullpunktene til en funksjon ved å se på grafen?
- Hvordan oppgir vi nullpunkter?
- Til grafen i oppgave 1: Hvilken form har grafen? Hva slags funksjonsuttrykk har slike grafer?
- Hvorfor er en funksjon som \(f(x)=(x+1)(x+4)\) en andregradsfunksjon?
- Hvordan kan du se på en parentes i funksjonsuttrykket om nullpunktet er et positivt eller et negativt tall?
- Hvordan må du tenke når du skal lage faktorer (parenteser) som gir et nullpunkt i en positiv x-verdi? Enn til et nullpunkt med en negativ x-verdi?
- Hva er en faktor?
- Hvorfor sier vi at funksjonsuttrykk som for eksempel \(f(x)=(x+1)(x+4)\) er faktorisert?
Mulig støtte
Denne aktiviteten er den fjerde i en serie om andregradsfunksjoner:
Ressursen er utviklet av Matematikksenteret