Andregradsfunksjoner III
Aktivitet
Gyldighetsområde, definisjonsmengde og verdimengde
I denne aktiviteten trenger du enten bruke firkantede tellebrikker eller ark med kvadratiske ruter.
Oppgaven handler om å lage ulike rektangler med omkrets 24. Hvis du bruker tellebrikker, regner du sidelengden til én brikke som 1. Hvis du tegner, skal du kun tegne rektangler med heltallige sidelengder.
Lag så mange ulike rektangler som du kan med omkrets 24. Skriv lengden (grunnlinja) og arealet av rektangelet inn i en tabell:
|
x |
1 | 2 | ... | ... | ||||
| y areal |
... |
Hvert av tallparene (x, y) fra tabellen skrives inn som punkter i Geogebra-appen nedenfor. Skriv i inntastingsfeltet for eksempel (1, 11) og trykk enter. Da markeres dette punktet i grafikkfeltet.
Du kan også bruke GeoGebra på din egen PC og skrive punktene inn der.
Nå skal du finne en graf som passer best mulig til punktene i grafikkfeltet. Hvilken form tror du grafen får?
I menyen finner du funksjonen «Kjeglesnitt gjennom fem punkt». Klikk på denne funksjonen, og deretter på fem punkt på grafen. Obs! Du må velge punktene i rekkefølge fra venstre mot høyre, og du bør velge punkter med litt avstand. Hva slags graf fikk du? Hva er funksjonsuttrykket til grafen?
Hva forteller grafen om arealet til ulike rektangler med samme omkrets? Hva slags rektangel har størst areal? Hva slags rektangel har minst areal?
Grafen ser ut til å ha funksjonsverdier i det uendelige både for negative og positive x-verdier. Men:
For hvilke x-verdier er denne grafen gyldig?
Hva er den minste x-verdien som er gyldig ut fra vår konkrete situasjon? Og hva er den største?
Hva er den minste og den største y-verdien som er gyldig ut fra vår konkrete situasjon?
Intervallet av gyldige x-verdier kalles funksjonens gyldighetsområde eller definisjonsmengde. Mens intervallet av gyldige y-verdier kalles funksjonens verdimengde.
Starthjelp
- Kan du lage et rektangel med lengde eller grunnlinje med lengde 1 og omkrets 24? Hva blir arealet?
- Kan du lage et rektangel med lengde/grunnlinje 2? Og 3?
- Hvilke lengder er det mulig å ha som grunnlinje?
- Når punktene tegnes opp, hvordan tror du grafen gjennom dem kommer til å se ut?
- Er det noen x-verdier eller y-verdier denne grafen ikke kan gjelde for?
Løsning
|
x |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| y areal |
11 | 20 | 27 | 32 | 35 | 36 | 35 | 32 | 27 | 20 | 11 |
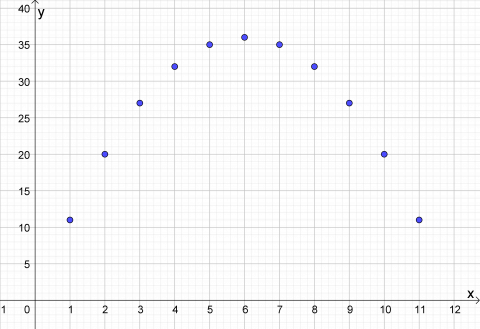
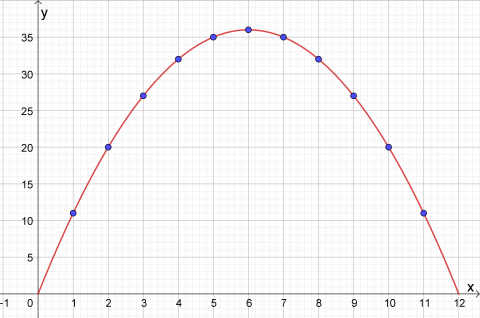
Nedenfor ser du hvordan punktene er plassert og hvordan grafen ser ut. Den er en parabel, så den er grafen til en andregradsfunksjon.
Hvis vi velger å kalle funksjonen f, har den funksjonsuttrykket \(f(x)=-x^2+12x\).
Vi ser at andregradsleddet har negativt fortegn, det gjør at grafen vender den hule siden ned, den har et toppunkt. Dessuten er konstantleddet \(c=0,\) grafen går gjennom origo.
MEN: Hvilke x-verdier er gyldige i vår situasjon?
- Hvis vi holder oss strengt til at vi bare kan bruke heltall i funksjonen, er den kun gyldig for de oppmerkede punktene. Da sier vi at definisjonsmengden til funksjonen f er \(D_f=\{1,2,3,4,5,6,7,8,9,10,11\}\). Dette er alle de mulige x-verdiene funksjonen kan ha. Og verdimengden er listen over alle mulige y-verdier som funksjonen kan ha: \(V_f=\{11,20,27,32,35,36\}\).
- Men hvis vi tenker oss at vi kan bruke alle tall som x-verdier, også desimaltall av alle slag, er det likevel begrenset. For lengden (grunnlinja) av rektangelet kan ikke bli 0, den må alltid være større enn 0 hvis vi skal ha et rektangel. Den kan heller ikke bli 12, den må alltid være mindre enn 12. Da er definisjonsmengden \(D_f=\langle0,12\rangle \) og verdimengden er \(V_f=\langle0,36\rangle\).
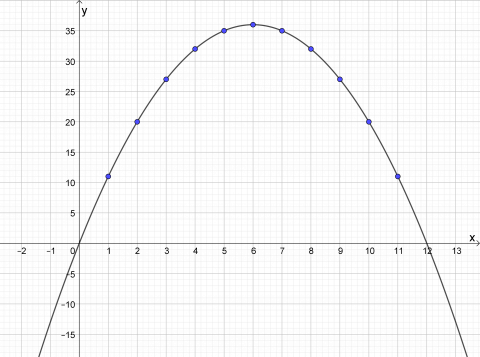
Vi kan tegne grafen i definisjonsområdet:
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
I denne aktiviteten får elevene lage en graf eller en kurvetilpasning til punkter de selv har fått fram gjennom et konkret arbeid. De vil få en graf de gjenkjenner formen til, og de får se at en graf kan inneholde informasjon om noe konkret, nemlig sammenhengen mellom omkrets og areal av et rektangel.
De får også se at grafen som tegnes i GeoGebra inneholder punkter som ikke passer inn i den konkrete situasjonen de har arbeidet med. Vi bruker denne aktiviteten til å introdusere begrepene gyldighetsområde, definisjonsmengde og verdimengde.
Mulig tilnærming
La elevene arbeide i par.
Gi dem oppgaven. Enten må de få kvadratiske tellebrikker å arbeide med, eller de kan tegne kvadrater på rutepapir. Da må de bare bli enige om hvor lang enhetslengden skal være før de begynner.
NB! Mange elever er vant til å tegne rektangler «liggende» og bruke begrepene «lengde og bredde» om rektangelets to sider. I denne aktiviteten må vi kalle rektangelets horisontale sider for «lengde» eller «grunnlinje», for vi ønsker rektangler med grunnlinjer fra 1 til 11.
Elevene har fylt ut tabeller og plottet punkter inn i koordinatsystem før, så det er kjent. De kan bruke appleten som er i aktiviteten, eller de kan bruke GeoGebra på egen PC. Eller de kan tegne på papir, om det passer best.
Når punktene er tegnet, kan det passe med en felles samtale i klassen. Har alle fylt ut tabellen? Hvilke tallpar fikk de? Var det noen problemer med å regne ut y-verdiene? Og når punkteten er plottet inn i koordinatsystemet, hva slags graf ser dette ut til å kunne bli?
Tegn grafen ved hjelp av funksjonen «Kjeglesnitt gjennom fem punkt». Da må man markere fem punkt, fra venstre mot høyre, og velge punkt med litt avstand. Hvis elevene jobber i GeoGebra kan de skrive x- og y-verdiene inn i regnearket, lage liste med punkt og utføre en regresjon ved å skrive RegPoly, skrive inn navnet på lista og graden på polynomet.
Ble funksjonsuttrykket som forventet? Hvis ikke, hva var ikke som forventet? La elvene diskutere, men sørg for at alle til slutt har samme andregradsfunksjon.
Hva er en graf? Slå fast følgende for hele klassen: En graf er en representasjon for en funksjon, den inneholder uendelig mange punkter. Alle punktene skal inneholde opplysninger som er sanne i forhold til funksjonen og i forhold til den konkrete situasjonen funksjonen skal beskrive.
Spørsmålet er: Inneholder denne grafen bare punkter som oppfyller disse kravene? Hvis ikke, hvilke punkter oppfyller kravene og hvilke gjør det ikke?
La elevparene få litt tid til å diskutere dette spørsmålet. Følg litt med på hvordan de tenker og prøv å fange opp elever som tenker ulikt. La flere løsninger presenteres for hele klassen. Noen vil si at siden vi jobber med brikker, er det bare punktene med heltallige x- og y-verdier som gir sann informasjon. Mens andre vil mene at vi kan lage rektangler med alle mulige lengder som er større enn 0 og mindre enn 12. Diskuter. Begge løsninger er riktige, men ut fra hvert sitt utgangspunkt.
Gode veiledningsspørsmål
- Hvilke lengder kan rektanglenes grunnlinje ha?
- Hvordan regner du ut arealene?
- Hvilke koordinatpar har du plottet inn?
- Hva slags graf tror du det blir når vi tegner en glatt kurve gjennom punktene?
- Hva slags funksjonsuttrykk tror du denne grafen har?
Mulig støtte
Denne aktiviteten er den tredje i en serie om andregradsfunksjoner:
- Andregradsfunksjoner I - Funksjonsuttrykk, faguttrykk, graf.
- Andregradsfunksjoner II - Sammenheng mellom funksjonsuttrykk og graf.
- Andregradsfunksjoner III - Gyldighetsområde, definisjonsmengde, verdimengde.
- Andregradsfunksjoner IV - Nullpunkter.
- Andregradsfunksjoner V - Faktorisering.
Ressursen er utviklet av Matematikksenteret