Andregradsfunksjoner II
Aktivitet
Sammenhengen mellom funksjonsuttrykk og graf
Den generelle formen for andregradsfunksjoner er \(f(x)=ax^2+bx+c\). Her er a, b og c koeffisienter, dvs. faste tall i funksjonsuttrykket, mens x er den frie variable.
I denne oppgaven kan du bruke GeoGebra-appleten ovenfor når du skal løse oppgavene. Du kan også velge å skrive ut oppgavene og bruke GeoGebra på egen PC, når oppgavene løses. Kopioriginal med oppgavene finner du her.
1.
- Finn ut hva koeffisienten c gjør med grafen ved å la a og b stå fast mens du varierer verdiene til c på glideren.
- Hva skjer med grafen? Hva forandres? Hvordan skjer forandringene? Og hva forandres ikke?
- Sett a og b fast på andre verdier, og kontroller om det du fant ut, fortsatt stemmer.
- Noter hvordan verdien av c påvirker grafen så detaljert som mulig.
2.
- Finn ut hva koeffisienten a gjør med grafen ved å la b og c stå fast mens du varierer verdiene til a på glideren.
- Hva skjer med grafen? Hva forandres? Hvordan skjer forandringene? Og hva forandres ikke?
- Sett b og c fast på andre verdier, og kontroller om det du fant ut, fortsatt stemmer.
- Noter hvordan verdien av a påvirker grafen så detaljert som mulig.
3.
- Finn ut hva koeffisienten b gjør med grafen ved å la a og c stå fast mens du varierer verdiene til b på glideren.
- Hva skjer med grafen? Hva forandres? Hvordan skjer forandringene? Og hva forandres ikke?
- Det kan være en hjelp å slå på Ekstremalpunkt, da vil det markeres et punkt på grafens topp- eller bunnpunkt. Deretter slår du på Sporing, da vil du få et spor som beskriver hvordan grafen beveger seg.
- Sett a og c fast på andre verdier, og kontroller om det du fant ut, fortsatt stemmer.
- Noter hvordan verdien av b påvirker grafen, så detaljert som mulig.
4.
I disse oppgavene skal du tegne noen grafer, bruk GeoGebra. Du kan også tegne for å kontrollere løsningene dine.
- Tegn grafen til funksjonen \(g(x)=2x^2+3x+1\). Hva kan du gjøre med funksjonsuttrykket for at grafen skal få et toppunkt i stedet for et bunnpunkt?
- Tegn grafen til \(h(x)=x^2-2x+4\). Hvordan må du endre funksjonsuttrykket hvis grafen skal beholde formen, men skjære y-aksen i \(y=-1\)?
- Hvordan vil funksjonsuttrykket til en andregradsfunksjon se ut hvis grafen skal gå gjennom origo? Finnes det flere løsninger?
- Tegn grafen til \(j(x)=x^2-4x+4\). Hvor mange nullpunkter har grafen? Hva kan du gjøre med funksjonsuttrykket for at grafen skal få to nullpunkter? Og hva kan du gjøre for at grafen ikke skal få nullpunkter i det hele tatt?
- Tegn grafen til \(k(x)=2x^2+2x\). Hva kan du gjøre med funksjonsuttrykket for at grafen skal bli smalere/brattere?
- Tegn grafen til \(t(x)=-x^2-2x+3\). Hva kan du gjøre med funksjonsuttrykket for at grafen skal bli mer åpen/mindre bratt?
- Tegn grafen til \(u(x)=2x^2-5x+4\). Hva kan du gjøre med funksjonsuttrykket for at grafen skal flyttes lenger til venstre?
Starthjelp
- For hver av oppgavene 1 – 3: Hvilke verdier vil du la de to koeffisientene som ikke skal endres, ha? Og hvilke verdier gir du koeffisienten du skal studere?
- Endrer grafens form seg? I tilfelle hvordan?
- Endrer grafens plassering seg. I tilfelle hvordan?
Løsning
1.
I er funksjonsuttrykkets konstantledd. Når \(x=0\) blir funksjonsverdien c, det betyr at grafen alltid skjærer y-aksen i \(y=c\).
Når c endres flyttes grafen oppover eller nedover, men grafens form forandres ikke.
2.
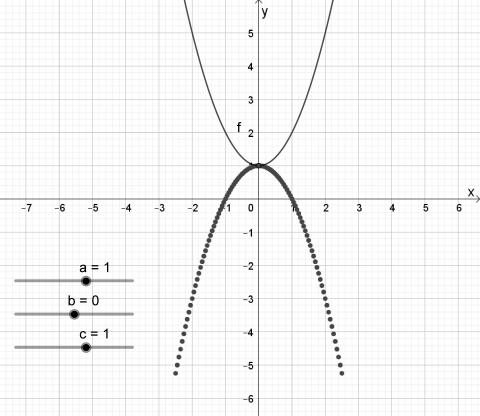
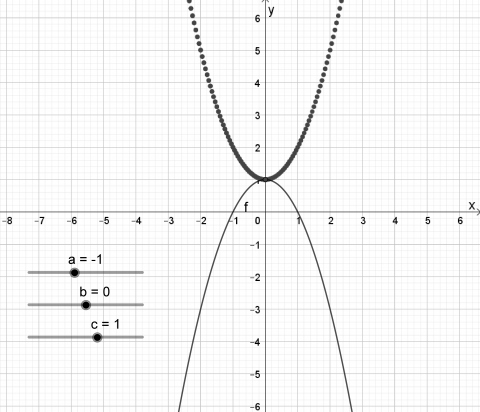
a er koeffisienten som står foran \(x^2\). Når a varierer, endrer grafens form seg. Når a er positiv, vil grafen vende den hule siden oppover, og den får et bunnpunkt. Når a er negativ vil grafen vende den hule siden nedover, og den får et toppunkt. Når tallverdien til a er et lite tall, er grafen vid, den har en ganske stor åpning. Men når tallverdien til a øker, blir grafen trangere eller brattere. Grafen forandrer form, men så lenge c ikke forandres, vil grafen skjære y-aksen i samme punkt, \(y=c\). Hvis \(a=0\), har vi ikke lenger noen andregradsfunksjon, og dermed heller ingen parabel. Grafen blir ei horisontal linje med likning \(y=c\).
3.
Når b varierer, endres ikke grafens form, men plasseringen endres. Grafen vil hele tiden gå gjennom punktet \(y=c\) på y-aksen. Når \(a>0\) og grafen har et bunnpunkt, vil grafen være høyest i koordinatsystemet når \(b=0\). Når b får økende positive verdier, flytter grafen seg nedover til venstre, og når b får økende negative tallverdier, flytter grafen seg nedover til høyre. Når \(a<0\) og grafen har et toppunkt, vil grafen være lavest i koordinatsystemet når \(b=0\). Når b får økende positive verdier, flytter grafen seg oppover til høyre, og når b får økende negative tallverdier, flytter grafen seg oppover til venstre. Hvis vi markerer grafens Ekstremalpunkt og sette på Sporing, kan vi få slike bilder:
Når b varierer, beveger grafen seg i en bane som er et speilbilde av parabelen selv.
4.
Merk: flere av disse oppgavene har flere enn én løsning.
- \(g(x)=-2x^2+3x+1\). Vi må ha minus foran andregradsleddet for at grafen skal få et toppunkt.
- \(h(x)=x^2-2x-1\). Når \(c=1\), vil grafen gå gjennom -1 på y-aksen.
- Hvis \(c=0\), går grafen alltid gjennom origo. Eksempel på løsninger er \(d(x)=x^2-3x \) og \(e(x)=-x^2+x\). (Funksjonsuttrykket mangler konstantledd.
- Grafen til \(j(x)=x^2-4x+4 \) har ett nullpunkt, den berører x-aksen i punktet (2, 0). Hvis \(c<4\), får grafen to nullpunkter, men hvis \(c>4\), får grafen ingen nullpunkter.
- Hvis grafen til \(k(x)=2x^2+2x \) skal bli smalere/brattere, må tallverdien av a bli større enn 2, for eksempel \(k(x)=4x^2+2x\).
- Hvis grafen til \(t(x)=-x^2-2x+3 \) skal bli mer åpen/mindre bratt, må tallverdien av a bli mindre enn -1. For eksempel \(t(x)=-0.5 x^2-2x+3\).
- For at grafen til \(u(x)=2x^2-5x+4 \) skal flyttes lenger til venstre, må b bli større enn -5, for eksempel \(u(x)=2x^2-3x+4\), da flyttes den oppover og til venstre. \(u(x)=2x^2+2x+4\), da har grafen også blitt flyttet oppover og til venstre, og har fått bunnpunktet på venstre side av y-aksen. \(u(x)=2x^2+5x+4\), her er grafen flyttet rett til venstre. Tegn og sjekk!
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Hensikten med denne oppgaven er at elevene selv skal oppdage en del sammenhenger mellom funksjonsutrykk og grafer til andregradsfunksjoner.
Mulig tilnærming
Elevene kan enten bruke oppgavene og appen som er i denne aktiviteten, eller de kan få utskrift av oppgavene på ark, som du finner her og bruke GeoGebra på egen PC.
La dem samarbeide i par. Alle skal skrive inn funksjonsuttrykket \(f(x)=a x^2 + bx + c\) og få fram glidere for a, b og c. Se til at alle får dette på plass før dere begynner med oppgavene.
La alle begynne med oppgave 1. Følge med på diskusjonene og se hvordan de angriper oppgaven. Hvis de er usikre, kan det være til hjelp å spørre om de kan forklare hva som forandrer seg og hva som ikke forandrer seg når c varierer.
Ta en samtale i samlet klasse etter oppgave 1. La elevene få forklare hva de har observert, hvis de har tenkt ulikt er det en fin anledning til å se grundigere på begrunnelsene de har, og ta elevene med på å vurdere. Sørg for at alle er enige om at konstantleddet c avgjør hvor grafen skjærer y-aksen, og dermed hvor «høyt eller lavt» grafen er plassert i koordinatsystemet. Og at konstantleddet ikke påvirker grafens form.
Arbeid tilsvarende med oppgave 2 og 3. Stopp etter hver oppgave slik at elevene får presentert løsninger, diskutert. Til slutt får dere slått fast hvilken betydning størrelsen på de to neste koeffisientene har for grafens form og plassering.
Når alle har etablert forståelse for hva de tre koeffisientene har å si for grafens form og størrelse, er de klar for oppgave 4. Til slutt, når de fleste har løst alle oppgavene, må dere ta en oppsummering i fellesskap.
Gode veiledningsspørsmål
- Hva skjer med grafen når du endrer verdien av c? Hva forandres? Og hva forandres ikke?
- Kan du undersøke hva som skjer hvis du velger andre verdier for de to koeffisientene som skal stå fast?
- Tilsvarende spørsmål for koeffisientene a og b.
Mulig utvidelse
Denne aktiviteten er den første i en serie om andregradsfunksjoner:
- Andregradsfunksjoner I - Funksjonsuttrykk, faguttrykk, graf.
- Andregradsfunksjoner II - Sammenheng mellom funksjonsuttrykk og graf.
- Andregradsfunksjoner III - Gyldighetsområde, definisjonsmengde, verdimengde.
- Andregradsfunksjoner IV - Nullpunkter.
- Andregradsfunksjoner V - Faktorisering.
Ressursen er utviklet av Matematikksenteret