Tre på rad – brøk og prosent
Aktivitet
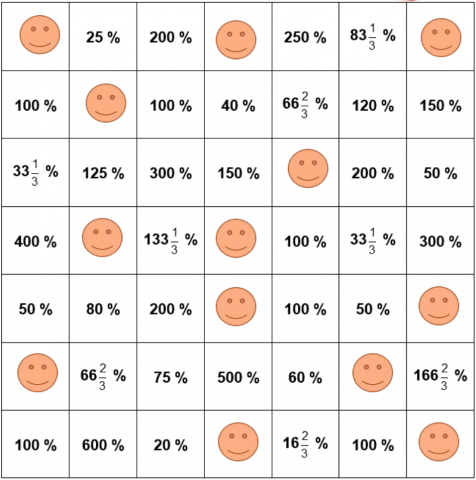
Dette spillet passer for 2–3 spillere. Hver spiller skal ha seks brikker i samme farge. De skal plasseres ut på spillebrettet underveis.
Spillerne kaster etter tur to terninger og lager en brøk der verdien på den ene terningen er teller, og den andre er nevner. Spilleren skal bedømme størrelsen på brøken han lager, finne prosenten som svarer til brøken, og til slutt legge en av brikkene sine på ei rute som viser denne prosenten.
Eksempel: Terningene viser \(3\) og \(4\). Du kan lage brøken \(3 \over 4\) og legge brikken på \(75\%\), eller \(4 \over 3\) og legge brikken på \(133 {1\over 3}\%\).
Dersom ingen ledige ruter passer til prosentene spilleren kan lage, legger hun/han brikken på en av rutene med smilefjes. Når alle spillernes brikker er lagt ut, fortsetter spillet ved at brikkene som står på brettet, flyttes til nye posisjoner, dersom spillerne får en annen brøk på brettet. Spillet fortsetter til en av spillerne har fått tre på rad: vannrett, loddrett eller diagonalt. Smilefjesene inngår i tre på rad.
Bruk vedlagte kopioriginal som spillebrett.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Hensikten med aktiviteten er å bedømme størrelsen på brøker og se sammenhengen mellom brøk og prosent. Elevene skal lage brøker ved hjelp av to terninger, og finne tilsvarende verdi uttrykt som prosent. De må argumentere for løsningene sine, gjerne ved å referere til erfaringsreferanser som null, en halv og en.
Mulig tilnærming
Spillet introduseres muntlig. Det kan være en fordel å vise hvordan spillet fungerer ved at du spiller mot elevene. Du skal ikke avsløre hvilke brøker og prosenter som hører sammen. Det skal elevene oppdage og utnytte i spillet. Dette er et spill som godt kan spilles jevnlig.
Gode veiledningsspørsmål
Det er fint om elevene får streve litt med dette spillet før de veiledes videre. Veiledningen bør være resonnerende og gjerne vendt mot svarene de allerede har funnet.
- Hvordan kan dere bruke det dere har funnet ut til å finne nye verdier av brøker og prosenter?
- Vil denne brøken være større eller mindre enn …?
- Kan vi se om brøken er større eller mindre enn en halv? En kvart? En hel?
- Har dere utforsket mulighetene ved å utvide eller forkorte brøker?
Mulig utvidelse
Lag et liknende spill som passer til andre typer terninger (for eksempel av typen 0–9, 1–12 eller 1–20). Tilpass spillbrettet til de nye brøkene. Finnes det prosenter som bør stå flere ganger?
Mulig støtte
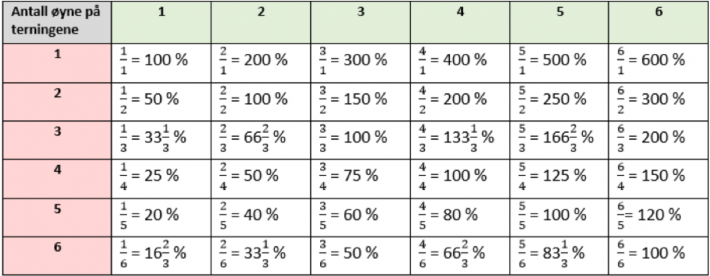
Det kan være en god støtte for enkelte elever å lage en tabell hvor de noterer hvilke brøker og prosenter som hører sammen. Tabellen kan struktureres etter størrelser på brøkene og prosentene, for eksempel slik:
Ressursen er utviklet av Matematikksenteret