Utforskning av rotasjon

Stikkord: Rotasjon

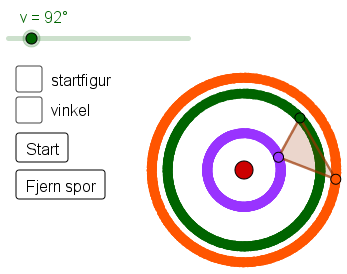
I GeoGebra-appleten nedenfor kan du bevege på glideren for å rotere figuren rundt det rødet punktet. Figuren kan også roteres automatisk ved å trykke på "Start"-knappen. Avkrysningsboksen "startfigur" bestemmer om den originale figuren vises eller ikke.

Prøv deg frem i appleten og noter noen tanker om:

Hvorfor tegnes det sirkler?
Hva betyr tallene på glideren?
Hvor ligger figuren hvis glideren står på \(90^\circ\) eller \(180^\circ\)?
Hva skjer om vi roterer med \(360^\circ\), \(540^\circ\) eller \(720^\circ\)?
Hvor er vinkelen som GeoGebra måler?
Vinkelen øker når vi drar glideren mot høyre, men hvorfor starter den på nytt etter \(360^\circ\)?

Etter at dere har diskutert spørsmålene ovenfor i klassen, arbeider du videre med å utforske rotasjonsegenskapene til likesidete mangekanter. Du kan bruke GeoGebra-appleten nedenfor på samme måte som den forrige, og du kan i tillegg endre hvor mange kanter mangekanten skal ha.

Må du alltid rotere \(360^\circ\) for at den roterte figuren skal dekke originalfiguren? Eksperimenter ved å flytte rotasjonssenteret utenfor, på, og inni figuren.
Hva er det minste antall grader du kan rotere en likesidet sekskant, et kvadrat og en likesidet trekant slik at den roterte figuren dekker originalfiguren?
Skriv en forklaring på hvorfor du mener at løsningen er riktig.
Hva er minste antall grader for en likesidet femkant?
Hva er minste antall grader for en n-kant?
Test hypotesen ved utprøving.

Hvorfor arbeide med denne oppgaven?

Målet med oppgaven er at elevene skal bli kjent med egenskapene til rotasjon. Oppgaven gir elevene mulighet til å oppdage hva som skjer når en figur roteres. Elevene skal utvikle forståelse for hva som skjer når vi roterer et objekt, hva som kjennetegner et rotasjonssymmetrisk objekt, hvordan de finner rotasjonssenteret til en slik figur, hva rotasjonsvinkel er, og hvordan de finner rotasjonsvinkelen.

Mulig tilnærming

Om det er lenge siden elevene har arbeidet med egenskapene til todimensjonale figurer (vinkler, kanter, hjørner), kan det være hensiktsmessig med en oppfriskning om dette før du introduserer problemene i denne oppgaven. Om du ikke vil at elevene skal bruke den ferdige GeoGebra-appleten med mangekanter, men at de heller skal lage figurene i GeoGebra selv, trenger de også å kunne tegne regulære mangkanter, måle vinkler og lage glidere i GeoGebra. Oppgaven legger godt til rette for verktøyopplæring i GeoGebra, men du må påberegne noe tid til dette i tillegg til arbeidet med oppgaven.

Begynn med å vise elevene den øverste GeoGebra-appleten. Animer glideren slik at trekanten roterer rundt det røde punktet, du kan enten bruke glideren for å endre rotasjonsvinkelen, eller trykke på Start-knappen for å animere glideren. Du kan velge om originalfiguren (startfigur) og rotasjonsvinkelen skal vises, i tillegg til den roterte figuren. Det er satt sporing på hjørnene til trekanten som roteres, slik at elevene kan følge bevegelsen til punktene. Det kan være lurt å stoppe animasjonen etter hvert, endre originalfiguren og animer glideren på nytt, slik at elevene ser at punktene beveger seg i en sirkel rundt rotasjonspunktet hver gang. La gjerne elevene bestemme hva som skal endres før animasonen starter på nytt, og be de forutse hva som kommer til å skje. Gi elevene litt tid til å utforske figuren på egenhånd, men pass på at de undersøker tilfeller hvor rotasjonssenteret er utenfor, på og innenfor figuren.

Diskuter i helklasse hva elevene har sett. Hvorfor tegnes det sirkler? Hva betyr tallene på glideren? Hovr ligger figuren hvis glideren står på \(90^\circ\) eller \(180^\circ\)? Her kan det også være lurt å spørre om hva som skjer når man roterer med \(360^\circ\), \(540^\circ\), eller \(720^\circ\). Disse vinklene er godt kjent for elever som liker snowboard eller skateboard, noe som gjør det lettere å knytte rotasjon til noe de kan fra før.

Etter klassediskusjonen ber du elevene arbeide videre i par eller små grupper med å utforske likesidede (regulære) mangekanter i GeoGebra. Elevene skal finne ut hvor mange grader de må rotere mangekanten for å få den roterte figuren til å dekke originalfiguren. Må de alltid rotere \(360^\circ\), eller er det mulig å rotere med en mindre vinkel? Elevene vil oppdage at plasseringen av rotasjonssenteret er avgjørende for at de skal kunne dekke originalfiguren ved å rotere med en vinkel som er mindre enn \(360^\circ\).

Om du vil at elevene selv skal lage figurene i et tomt GeoGebra-vindu, kan det være lurt å be de lukke nettsiden som inneholder den ferdige appleten. Trykk her for å skrive ut spørsmålsark til elevene.

Det er viktig at elevene får prøve (og feile) uten at vi kommer med løsningene. Slik blir de både bedre problemløsere, samtidig som verktøykunnskapen i GeoGebra utvikles.

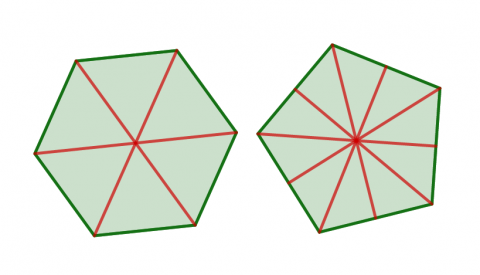
Elevene løser problemet ved utforsking. Først må de finne ut hvilken betydning plasseringen av rotasjonssenteret har, og hva som skjer når de roterer med ulike vinkler. Deretter må de diskutere og resonnere seg fram til hvorfor akkurat disse vinklene fungerer når rotasjonssenteret er plassert i midten av mangekanten. Etter å ha argumentert for løsningene sine, skal de finne en generell regel som gjelder for alle likesidede mangekanter når rotasjonssenteret er plassert i midten av figuren. Elevene vil også oppdage at det er enklere å finne midtpunktet hvis antall sider i mangekanten er et partall enn et oddetall (se bildet nedenfor). Hvorfor er det slik?

Regulær sekskant og regulær femkant med linjestykker gjennom midtpunkt

Som oppsummering kan elevene vise fram hvordan de har tenkt, og hvilke matematiske sammenhenger de har funnet. Velg ut elever som skal presentere arbeidet sitt basert på observasjonene som er gjort underveis. Det er viktig å velge ut elever som har brukt forskjellige løsningsmetoder. Pass samtidig på å forklare og ta i bruk relevante matematiske begreper som rotasjonssymmetrisk, rotasjonssentrum og rotasjonsvinkel.