Kompistall
Aktivitet
Se på denne tallrekken:
10 15 21 4 5
Tallrekken er slik at hvis du adderer to tall som står ved siden av hverandre, blir summen et kvadrattall:
10 + 15 = 25
15 + 21 = 36
21 + 4 = 25
4 + 5 = 9
Kan du lage en tallrekke med alle tallene fra 1–17, slik at summen av to tall som står ved sidene av hverandre, blir et kvadrattall?
Du kan skrive ut tallene ved å laste ned kopioriginal. De kan være til hjelp for å teste ut ulike tallrekker.
Kan du lage flere forskjellige tallrekker med de samme tallene? Hvis ikke, kan du være helt sikker på at løsningen din er unik?
Starthjelp
Er det noen tall som kan adderes med bare ett tall for at summen skal bli et kvadrattall?
Hvor i så fall skal disse tallene plasseres?
Løsning
Én måte å løse denne oppgave på er å sette opp alle kvadrattallene til og med 33, siden 16 + 17 = 33 er det største tallet vi kan få.
1 – 4 – 9 – 16 – 25
Det betyr at for 17 og 16 er det bare én mulighet nemlig 25, så de må stå i hver sin ende. 16 adderes med 9 og settes i den ene enden. 17 må adderes med 8, og 8 må adderes med 1 siden det er bare ett 8-tall. Etter 1 er det to muligheter, både 3 og 15 vil fungere, men ettersom 15 bare går an med 1 og 10, må 15 settes her, og så 10. Deretter er det bare én løsning for hvert nytt tall til vi til slutt har denne rekken:
16 – 9 – 7 – 2 – 14 – 11 – 5 – 4 – 12 – 13 – 3 – 6 – 10 – 15 – 1 – 8 – 17
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
I denne aktiviteten må elevene må tenke strategisk og utarbeide overbevisende argumenter og begrunnelser for funnene sine. For å kunne gjøre denne aktiviteten bør elevene imidlertid ha kunnskaper om kvadrattall.
Mulig tilnærming
Introduser problemet ved å bruke eksemplet 10, 15, 21, 4, 5, og forklar at denne tallrekken er spesiell, fordi hvert par addert gir et kvadrattall. Så skal elevene parvis eller i grupper på tre lage en lignende tallrekke ved å bruke tallene fra 1 til 17. Del gjerne ut disse tallene som de kan bruke som konkreter.
Når parene eller gruppene begynner å finne de første løsningene, kan du informere elevene om at du ønsker å vite alle mulige måter å lage en slik tallrekke på. Utfordre dem til å utarbeide overbevisende argumenter som forklarer at de har funnet alle mulige måter.
På slutten av aktiviteten bør elevene få mulighet til å vise framgangsmåtene og løsningene sine til hverandre.
En alternativ måte å begynne aktiviteten på er å spørre 17 frivillige om å stille seg opp på en rekke og holde et tall hver. Deretter skal resten av klassen plassere dem slik at tallrekken følger kriteriene som gitt i oppgaven. Når elevene har funnet en løsning, kan de arbeide i par for å forsøke å finne nye løsninger og utarbeide argumenter for at de har funnet alle.
Gode veiledningsspørsmål
- Er det noen tall som ikke kan stå sammen?
- Er det noen tall som bare kan stå sammen med ett tall?
- Er det noen tall som bare kan stå sammen med to tall?
- Er det noen tall som kan stå sammen med flere enn to tall?
- Hvordan kan du være sikker på at du har funnet alle mulige løsninger?
Mulig utvidelse
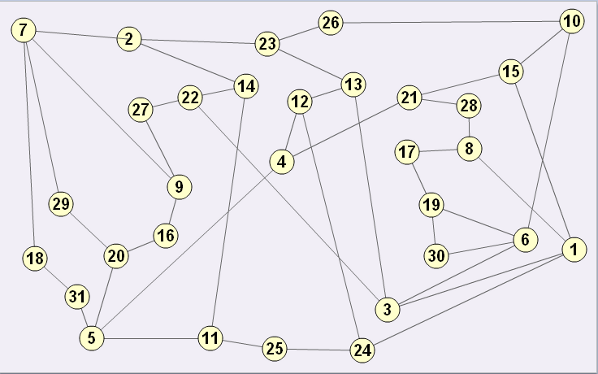
Grafen under har punkter med nummer fra 1 til 31. Hver linje knytter sammen to tall, og hvis du adderer de to tallene, får du et kvadrattall.
Bruk grafen til å lage en tallinje med tallene 1–31 slik at tallene som står sammen to og to, gir et kvadrattall til sum. Finnes det mer enn én løsning?
Kan du finne et hvilket som helst annet tall n mindre enn 31 som gjør at alle tallene fra 1 til n kan danne en tallinje på samme måte? Hvordan kan grafen være til hjelp?
Mulig støtte
Foreslå for elevene at de kan lage en tabell der de kan notere tallene som addert gir et kvadrattall.
Illustrasjonsfoto: Kyle Hinkon on Unsplash
Ressursen er utviklet av NRICH