En mystisk tabell
Aktivitet
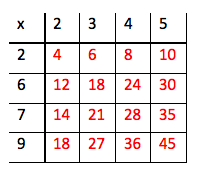
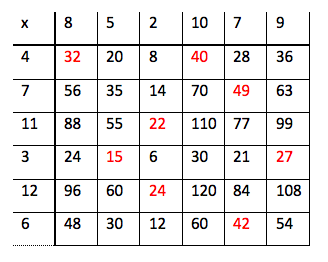
Se godt på denne tabellen:
Kan du se hvordan denne tabellen fungerer?
Hvorfor er noen tall røde og andre svarte?
Kan du forklare hvorfor det røde 6-tallet står i akkurat den ruta?
Hvorfor står det 45 i den nederste ruta til høyre?
Du ser kanskje at det er tallene fra 2 til 9 som er brukt for å lage tabellen, og at 2 er det eneste tallet som er brukt to ganger.
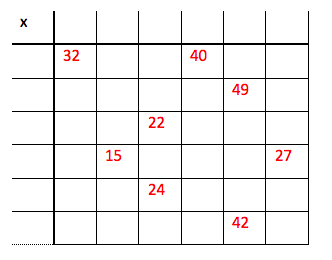
Klarer du å fylle ut tabellen under?
Her er det tallene fra 2 til 12 som danner tabellen, og også denne gangen er det bare ett tall som brukes to ganger.
Her finner du en utskriftsvennlig versjon av tabellen.
Starthjelp
Finn ut hvilket tall som er brukt to ganger. Det kan hjelpe deg videre.
Løsning
Viktoria og Nora har studert den første tabellen og funnet ut dette:
- Vi ser hvordan tabellen fungerer. De svarte tallene i kolonnene nedover og radene bortover multipliseres og gir et rødt tall i «ruta der de møtes». Svart tall ∙ svart tall = rødt tall. De røde tallene er svar på multiplikasjonsstykkene.
- Vi ser at den røde sekseren står i akkurat den ruta fordi 2 ∙ 3 = 6.
- 45 står i den nederste ruta til høyre, for der møtes 5 og 9, og 5 ∙ 9 = 45.
- Da vi skulle arbeide med den andre tabellen, brukte vi litt tid på å finne ut hvilke multiplikasjonsstykker som kunne gi de forskjellige røde tallene i tabellen. Vi visste at det er bare 7 ∙ 7 som blir 49. Da kunne vi plassere 7 i femte kolonne og andre rad.
- Vi visste også at 6 ∙ 7 er 42. Dermed kunne vi plassere 6 i den nederste raden.
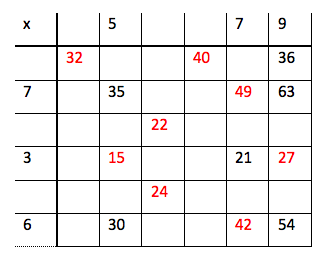
- Det er bare 3 ∙ 9 som gir 27. Derfor måtte 3 stå i fjerde rad, for det er ingen ting i 9-gangen som blir 15. Da måtte 9 stå i den siste kolonnen og 5 i den andre kolonnen. Tabellen ble slik:
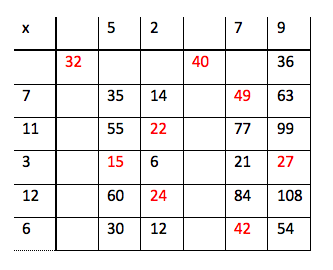
7. Tallet 22 kan bare lages av 2 ∙ 11. Da vet vi at 11 må stå i tredje rad, fordi det er ingen ting i 11-gangen som blir 24. 2 må stå i tredje kolonne. Og dermed må 12 stå i femte rad. Dermed ser tabellen slik ut:
8. Nå er det tre tall vi ikke har brukt: 4, 8 og 10. 4 ∙ 8 er 32. Da vet vi at 10 må stå i den fjerde kolonnen. Vi vet også at 4 må stå i første rad og 8 i første kolonne. Den utfylte tabellen blir slik:
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
For å oppmuntre elevene til å være nysgjerrige kan du presentere dem for en utfordring som de kan prøve å løse, eller en spennende kontekst som krever forklaring.
Denne oppgaven krever at elevene bruker kunnskap de har om multiplikasjon, kvadrattall og primtall. Arbeid med problemet vil også øke elevenes kjennskap til representasjon av multiplikasjon i tabeller.
Mulig tilnærming
Begynn med å gi hele klassen tall som 18, 33, 35, 48 og 56, og spør om de kjenner noen multiplikasjonsstykker som gir disse tallene. Inkluder deretter noen kvadrattall, slik som 25, 36 og 49.
Deretter introduserer du den første tabellen. Her kan det være lurt å diskutere hvordan tabellen fungerer, og spørsmålene som er knyttet til tabellen. Pek på at den røde fireren er et resultat av 2 ∙ 2, altså et kvadrattall. Hva er spesielt med kvadrattallene? Finnes det flere kvadrattall i denne tabellen?
Nå kan elevene arbeide med å fylle ut den første tabellen i par. Mens du går rundt og observerer, kan du spørre hvordan de vet hvor de ulike tallene skal stå. Hvordan holder de oversikt over hvilke tall de har brukt?
En alternativ tilnærming er å gi elevene en ferdig utfylt tabell (den første), og la dem undersøke hvordan den fungerer.
Før dere går videre til den andre tabellen, er det lurt med en klassediskusjon der dere prøver å komme fram til at tabellen representerer ulike multiplikasjonsfakta. Det vil hjelpe elevene til å fylle ut den andre tabellen.
Etter dette kan elevene to og to begynne å utforske problemet med den andre tabellen. Du finner en kopioriginal med tabellen her.
Mot slutten av økta kan du samle klassen igjen og diskutere hvordan de har løst oppgaven. Hva gjorde de for å komme i gang? Hvordan fant de ut hvor de ulike tallene skulle stå?
Gode veiledningsspørsmål
- Hvor kan dere starte? Hvorfor?
- Hvordan kan dere avgjøre hvilket tall som er brukt to ganger?
- Hvilke multiplikasjonsstykker gir de ulike svarene? Kan det være flere?
- Hvordan kan dere holde oversikt over hvilke tall dere har brukt?
- Er det noe dere blir nysgjerrige på?
Mulig utvidelse
Elevene kan lage lignende utfordringer til hverandre. Hvor lite informasjon kan det stå i tabellene uten at det blir umulig å løse dem?
Mulig støtte
Noen elever kan ha nytte av å begynne med å finne ut hvilket tall som er brukt to ganger. Oversikt over den lille multiplikasjonstabellen kan også være nyttig.
Ressursen er utviklet av NRICH