Partall og oddetall
Aktivitet
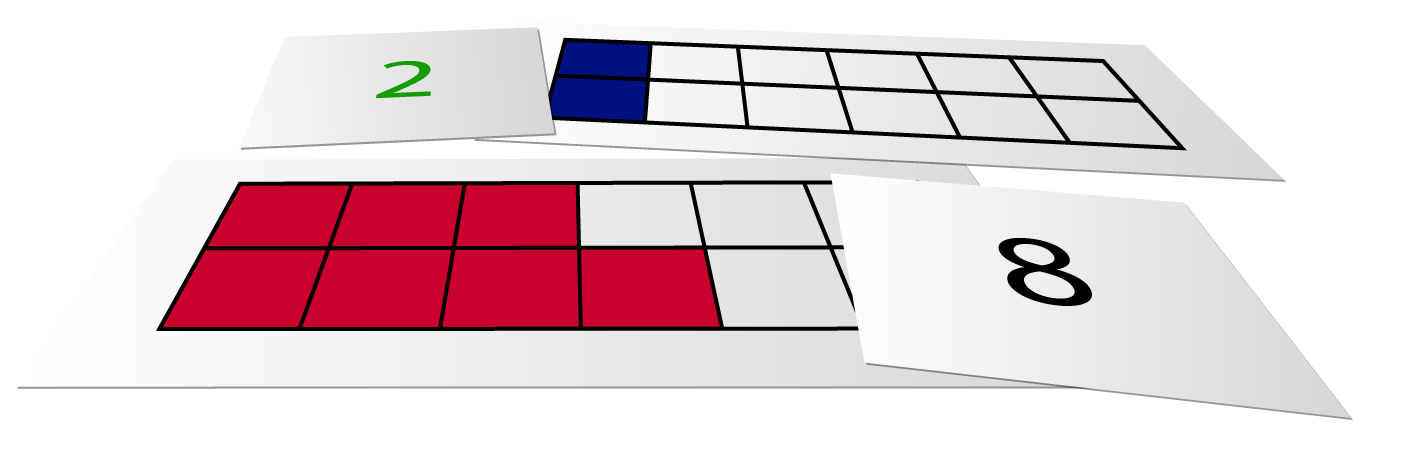
Denne aktiviteten fungerer best når den gjennomføres i hel klasse eller i en stor gruppe, delt inn i fire mindre grupper. Hver av gruppene får en kopi av de svarte kortene, de blå kortene, de røde kortene eller de grønne kortene.
Hver gruppe trenger et sett med kort i sin farge (samme som gruppas farge). Kopioriginaler for svarte kort, blå kort, grønne kort og røde kort finner dere i listen over kopioriginaler til venstre.
Gruppene legger kortene sine slik at hvert tallkort ligger ved siden av det kortet som har samme antall fargede kvadrat.
Bruk klosser som kan settes sammen, for eksempel multilink eller centikuber, og bygg tallene på de kortene dere har. Her ser dere en blokk som viser 9:
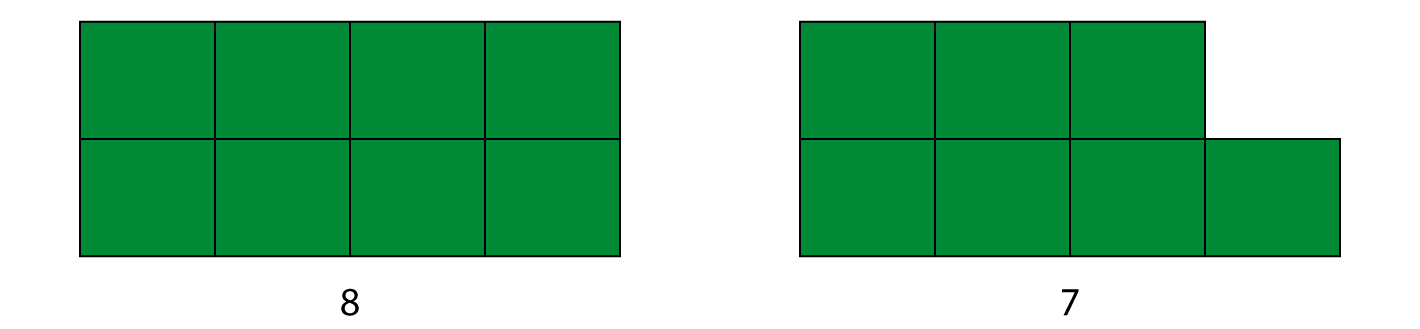
9 er et oddetall. Kan dere se det ut fra formen på blokken? 8 er et partall. Blokken for 8 er annerledes enn blokken for 9. Hva er forskjellen?
Velg to av tallene som dere har bygd. Hvilken type tall får dere når dere adderer dem ved å sette sammen de to blokkene? Er det et oddetall eller et partall?
Velg to andre tall, og adder dem på samme måte. Hvilken type tall får dere denne gangen, partall eller oddetall?
Prøv dette på mange ulike måter og med de ulike blokkene deres. Hva ser dere?
Hvordan kan dere notere funnene deres?
Når får dere et oddetall?
Når får dere et partall?
Finner dere et mønster eller system? Kan dere forklare hvorfor det blir sånn?
Starthjelp
Hvis dere ikke har multilink eller centikuber, kan dere bruke bildene av de fargelagte papirblokkene i kopieringsoriginalene. Klipp ut de ulike blokkstørrelsene, og velg blokker som dere setter sammen.
Løsning
Dette er en artig oppgave som handler om partall og oddetall. Den involverer både addisjon, telling og generalisering. Ved å arbeide med denne aktiviteten kan elevene oppdage noen generelle regler som kan være veldig nyttige i andre oppgaver.
Mathias og Hanna har kommet fram til følgende løsning:
Partall har to like lange rader med klosser når vi bygger dem, mens oddetall har en ekstra kloss på den ene raden. Slik er alle tallene, både partall og oddetall.
Når du adderer et oddetall (med en ekstra kloss) med et partall (uten en ekstra kloss), vil det nye tallet bli et oddetall (med en ekstra kloss).
Når du adderer to partall (uten ekstra klosser), vil det nye tallet bli et partall (uten ekstra klosser).
Når du adderer to oddetall, vil det nye tallet bli et partall, fordi de to ekstra klossene danner et nytt par.
O = oddetall, P = partall
O + O = P
P + P = P
P + O = O
Tre oddetall vil bli et oddetall, for da blir det igjen en ekstra kloss.
Fire oddetall vil bli et partall, for da blir det to nye par med klosser fra de fire ekstra klossene.
Lærerveiledning
Hva ønsker vi med denne oppgaven?
Aktiviteten er designet for arbeid i grupper, slik at elevene får se mange eksempler. Den gir dem mulighet til å konsolidere telling og addisjon, og samtidig erfaring med ulike representasjoner av partall og oddetall. Målet er at elevene skal kunne generalisere resultatene av addisjon med partall og oddetall.
Mulig tilnærming
La elevene samarbeide om å pare kortene, slik at hvert tall ligger sammen med det kortet som viser samme antall fargete kvadrat. Deretter gir du gruppene klosser (multilink, centikuber e.l.) og utfordrer dem til å bygge modeller av hvert tall slik at modellene ligner på bildene av de fargete kvadratene. Det kan hende du må demonstrere dette for elevene, og da er det viktig at du setter sammen kubene slik at de former to rader, slik som med tallet 9:
Samle klassen og be en av gruppene om å velge to av tallblokkene sine. Hold opp de to blokkene, og spør elevene om noen kan addere tallene. Hvor mange klosser blir det til sammen? Be noen vise hva de gjør, og forklare hvordan de tenker. Det kan komme ulike forslag til hvordan en kan sette sammen de to blokkene. Bruk tid på å utforske det. Hvilken måte gjør det enklest å telle det totale antallet klosser? Lytt til elevenes forklaringer, og trekk fram strategier der de teller toere. Det er enklest hvis blokkene er basert på to rader med klosser. Her adderes 9 og 11:
Nå skal gruppene undersøke summen av ulike par av tall ved å bruke blokkene de har laget. Elevene noterer ned det de finner ut. De kan tegne, skrive, bruke klossene eller fargelegge ruteark.
Etter at elevene har undersøkt summen av ulike tallpar, samler du dem igjen og sier at du har satt sammen to blokker akkurat som de har gjort. Den nye blokken du fikk, hadde 15 klosser. Spør elevene om de kan finne ut hvilke to tall (blokker) du kunne satt sammen. Mens elevene kommer med forslag, tegner du representasjoner av forslagene deres, for eksempel slik:
Tegn flere eksempler på tavla, og spør elevene hva de legger merke til. Hva er likt ved alle eksemplene? Lytt til elevenes observasjoner, og få tydelig fram de bidragene som handler om at noen tall får blokker som har en ekstra kloss som stikker ut, mens andre tall får blokker som er rektangulære – de mangler en kloss som stikker ut. Hvis elevene ikke kjenner begrepene partall og oddetall, introduserer du dem. Hvilken type tall er 15? La elevene sette ord på at når vi adderer et oddetall og et partall, får vi et oddetall (eller at vi kan lage et oddetall ved å addere et partall og et oddetall).
Gjenta den samme prosessen med et partall, for eksempel 12. Hvilke to tall kan vi addere og få 12? Tegn eksempler på tavla, og la elevene generalisere på samme måte: Et oddetall addert med et oddetall gir et partall, og et partall addert med et partall gir et partall (eller at vi kan få et partall ved å addere to oddetall, eller ved å addere to partall).
Gode veiledningsspørsmål
- Hvordan vil dere sette sammen kortene/blokkene?
- Kan kortene/blokkene settes sammen på forskjellige måter?
- Hvilke tall har dere allerede prøvd?
- Fortell om det dere har tegnet og skrevet. Hva ser dere der?
- Ser dere noen systemer i det dere har funnet ut?
Mulig utvidelse
Gjør en lignende undersøkelse med subtraksjon. Hva finner dere da?
Hvis dere har bare enere, treere og femmere (men kan bruke som mange dere vil av hver sort), kan dere da lage 12 ved å bruke fire tall? Kan dere finne en måte å lage 13 på? Svarer elevene raskt nei på det siste spørsmålet, kan du anta at de har forstått generalisering omkring addisjon av partall og oddetall.
Mulig støtte
Hvis det er nok multilink-klosser eller centikuber, kan enkelte elever bygge og bruke modeller av alle tallene i stedet for å tegne løsninger på papir.
Ressursen er utviklet av NRICH