Skredder og skjerf
Aktivitet
En skredder har seks meter stoff og skal sy skjerf.
a) Til hvert skjerf trenger han \(1 \over 2\) meter stoff. Hvor mange skjerf kan han sy?
b) Skredderen skal sy en annen type skjerf som er slik at det trengs \(1 \over 4\) meter stoff for hvert skjerf. Blir det flere eller færre skjerf enn i sted? Kan du finne ut hvor mange skjerf det blir uten å regne på nytt? Forklar og begrunn.
c) For en tredje type skjerf trengs det \(3 \over 4\) meter stoff til hvert skjerf. Blir det flere eller færre skjerf enn i b)? Blir det flere eller færre skjerf enn i a)? Kan man finne ut hvor mange skjerf det blir uten å regne (helt) på nytt? Forklar og begrunn.
Tillegsspørsmål:
Hvor mye blir 10 : \(5 \over 4\) og hvordan finner du ut det? Hva slags situasjon/regnefortelling passer til det regnestykket?
Opplegget er utviklet i forbindelse med MAM (Mestre Ambisiøs Matematikkundervisning)
Løsning
Her går det an å tenke på mange måter. Under er noen forslag:
a) Skredderen trenger \(1 \over 2\) meter per skjerf.
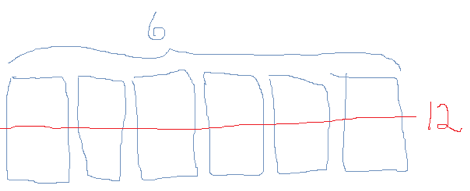
- Man kan lage en tegning av seks meter stoff (som på bildet under), dele alle i to og få tolv biter på \(1\over 2\) meter.
- \(6: {1 \over 2} =12\)
b) Skredderen trenger \(1 \over 4\) meter per skjerf
- Skjerfene blir kortere så vi har stoff nok til flere skjerf. Siden de nye skjerfene er halvparten så lange som skjerfene i a) blir det dobbelt så mange, altså 24.
- \(6: {1 \over 4}=24\)
c) Skredderen trenger \(3 \over 4\) meter per skjerf
- Det blir ett skjerf per meter stoff, med en rest på \(1 \over 4\) meter. Til sammen blir det \(6 \over 4\) meter med rest, som er nok til 2 skjerf på \(3 \over 4\) meter. Så skredderen får 6 skjerf, pluss de 2 skjerfene han får laget av «restene». Han får laget 8 skjerf.
- \(6: {3 \over 4}=8\)
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Hensikten med aktiviteten er å se på ulike løsningsstrategier i divisjon (målingsdivisjon) og sammenhengen mellom disse strategiene. Oppgavene legger til rette for at en kan ha spesielt fokus på hva som skjer med svaret når divisor minker/øker med en gitt faktor. Elevene får utforske divisjon med brøk ved hjelp av ulike representasjoner – tegninger/konkreter, tallinje, symboler.
Spørsmålene er knyttet til antall skjerf skredderen kan sy. Det er ikke opplagt for elevene at de i denne konteksten bruker divisjon. Mange elever knytter divisjon til en mengde de deler likt, med etterfølgende spørsmål: Hvor mye blir det på hver? Denne formen for divisjon kaller vi delingsdivisjon. I denne oppgaven er spørsmålet: Hvor mange skjerf kan skredderen sy? Mange elever vil tenke at skredderen får to skjerf på en meter. De finner løsningen, 12 skjerf, ved å multiplisere seks med to. Utfordre elevene til å reflektere rundt regnearten de velger og hva regnestykket forteller. Hva er det sekstallet representerer? Hva med totallet? Hvor er tallet \(1 \over 2\)?
Mulig tilnærming
Oppgave a) kan presenteres muntlig for elevene. Elevene arbeider parvis og uttrykker løsningsforslagene sine skriftlig. Kan oppgaven løses på flere ulike måter? Ulike løsningsstrategier bør løftes fram i en felles diskusjon. Du kan notere de ulike framgangsmåtene på tavla. Utfordre elevene til å argumentere for sine svar.
Presenter også de to neste oppgavene muntlig for elevene. Utfordre elevene på om de kan finne løsninger uten å starte helt på nytt igjen, og begrunne disse. Elevene arbeider fortsatt parvis og utarbeider forslag på store ark/plakater slik at løsningene kan presenteres for de andre elevene i klassen. Elevene forklarer og begrunner. Oppfordre elevene til å bruke ulike representasjoner.
Observerer arbeidet og velg rekkefølgen på presentasjonene. Diskusjon og oppsummering kan etter hvert fokusere på regneoperasjon og hvilke regnestykker som gir svar på problemstillingene. Å vurdere/diskutere at svarene blir større når vi bruker divisjon vil være viktig. Mange elever tror jo at multiplikasjon gir større tall og divisjon gir mindre tall.
Gode veiledningsspørsmål
- Hva vil skredderen gjøre med tøystykket på seks meter?
- Hvordan vil dere forklare framgangsmåten deres for de andre i klassen?
- Kan dere vise løsningen ved hjelp av andre representasjoner (tegninger/konkreter, tallinje, symboler).
- Ser dere noen sammenheng mellom de ulike oppgavene?
- Hvilken regneart passer til oppgaven?
- Hvilket regnestykke beskriver situasjonen? Hva forteller regnestykket?
- Hva hvis skredderen brukte tre meter per skjerf? Hvilket regnestykke ville passe til oppgaven? (tre går to ganger opp i seks)
- Hva hvis han brukte en meter per skjerf? (en går seks ganger opp i seks)
- Hva ble regnestykket da han trengte ½ meter per skjerf? Forklar og begrunn. (\(1 \over 2\) går 12 ganger opp i seks)
Mulig støtte
Elever vil kunne ha nytte av målebånd og eventuelt hyssing i arbeidet med denne oppgaven. Tegning vil også være en god støtte i arbeidet. Dersom elever strever med å se at det er divisjon de driver med, kan det være en god ide å gå veien via divisjon med heltall. Du kan spørre dem hvordan regnestykket blir om skredderen syr skjerf som er 2 eller 3 meter lange. Da kan det være lettere å overføre strategien til skjerfene som skal være \(1 \over 2\) meter lange også.
Ressursen er utviklet av Matematikksenteret