3 x 3 areal
Problem
Hvilken av de fargede figurene har et areal som er ulikt de fire andre?
Starthjelp
- Kan du finne arealet av de fargede områdene, eller arealet av de hvite områdene utenfor?
- Kan du halvere arealet av noen rektangler?
Løsning
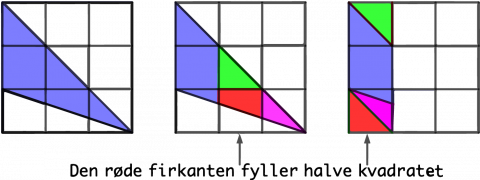
Vi kan tegne eller klippe opp arealene i figurene for å se hvor mange ruter hver av dem vil fylle:
Figur A: Figuren vil fylle 3 ruter, den har areal 3.
Figur B: Figuren vil fylle 3 ruter, den har areal 3.
Figur C: Figuren vil fylle 3 ruter, så arealet er 3.
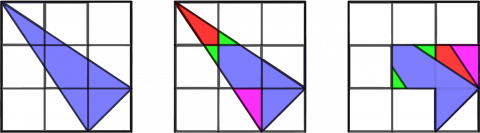
Figur D: Hvis vi deler opp denne figuren og prøver å fylle ut flest mulig ruter, ser vi at den bare fyller opp \(2\frac12\) rute. Denne figuren må derfor skille seg fra de andre, siden figur E også fyller 3 ruter.
Ressursen er utviklet av NRICH
8,9