Fargelegg symmetrier
Aktivitet
Karl laget et symmetrisk mønster ved å fargelegge fire felt i et 3 · 3 kvadratisk rutenett.
Alise laget et symmetrisk mønster ved å fargelegge to felt i et 3 · 3 isometrisk rutenett.
Velg om du vil arbeide med kvadratisk rutenett eller isometrisk rutenett.
Hvor mange forskjellige symmetrier kan du lage?
Her er noen spørsmål du kan tenke over og prøve å finne svar på:
- Hvor mange forskjellige mønstre kan du lage hvis du får lov til å fargelegge bare ett felt?
- Hvor mange forskjellige mønstre kan du lage hvis du får lov til å fargelegge to felt, tre felt, fire felt?
- Er det noen sammenheng mellom mønster med seks fargede felt og mønster med tre fargede felt? Hva slags sammenheng mener du det er i så fall? Finner du sammenhenger mellom andre mønster?
- Kan du lage mønstre med bare én symmetrilinje?
- Kan du lage mønstre med to symmetrilinjer, med tre symmetrilinjer eller med fire symmetrilinjer?
- Kan du lage mønstre som har både rotasjonssymmetri og symmetrilinjer?
- Kan du lage mønstre med rotasjonssymmetri som ikke har symmetrilinjer?
- Kan du lage mønstre med flere farger?
Starthjelp
- Begynn med å se på alle mulighetene for mønster med bare ett fargelagt felt.
- Fortsett med to felt, så tre felt, osv.
Løsning
Det er mye å tenke på i denne oppgaven. Du må arbeide systematisk for å unngå å lage samme mønster to ganger, eller for å glemme et mønster!
Først viser vi løsninger i trekanter i isometrisk rutenett.
Det er viktig å bli enige om hva man mener med forskjellige mønster.
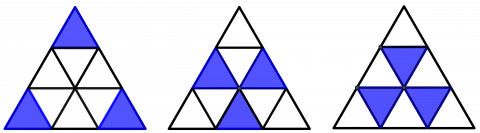
Dere må bli enige om dere skal regne de tre figurene nedenfor som samme løsning eller som tre ulike løsninger. Alle har én symmetrilinje, men hver figur er rotert i forhold til den forgående, så her er det rotasjonssymmetri.
1. Løsning med ett farget felt i isometrisk rutenett:
Dette er 3 eller 9 ulike løsninger (etter som vi regner med rotasjonssymmetri eller ikke).
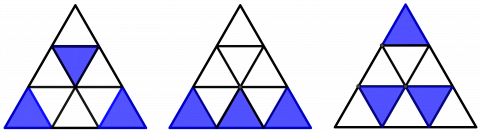
2. Løsning med to fargede felt
Det er 6 ulike løsninger med to fargede felt, eller 18 hvis vi regner med rotasjonssymmetriene.
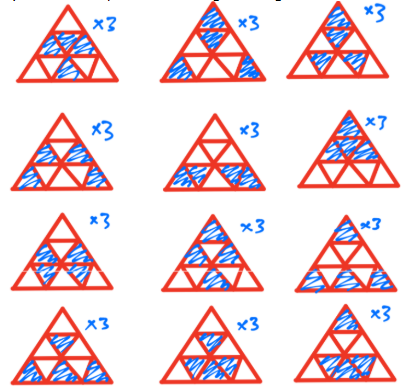
3. Løsning med tre fargede felt
Med tre fargede felt er det 10 ulike løsninger med én symmetrilinje. Hvis vi teller med alle rotasjonene, vil de tre første figurene være de samme om de blir rotert, mens de sju siste kan roteres og gi tre ulike bilder hver. Hvis vi regner med rotasjonene, blir det altså 3 + 7 ∙ 3 = 24 ulike løsninger.
4. Løsning med fire fargede felt
Det er 12 mulige måter å fargelegge fire felt på, eller 36, hvis vi teller med rotasjonene.
Hva er sammenhengen mellom et mønster med seks fargelagte felt og et med tre fargelagte felt?
I alle trekantene er det 9 felt. Det å fargelegge 2 felt og ha 7 hvite felt tilsvarer det å fargelegge 7 felt og la 2 være hvite. Det vil gi tilsvarende løsninger.
På samme måte vil det være med 3 fargede og 6 hvite felt, og med 6 fargede felt og 3 hvite.
Hvor mange symmetrilinjer?
Legg merke til at alle løsningene med to fargede felt har bare én symmetrilinje.
Noen av løsningene med tre fargede felt har både tre symmetrilinjer og rotasjonssymmetri.
Kan du finne figurer med to symmetrilinjer? I tilfelle, hvordan? I tilfelle ikke, hvorfor ikke?
Løsninger i kvadratisk rutenett:
Kvadratet kan ha symmetrilinjer i begge diagonalene og i vannrett og loddrett linje gjennom midten av kvadratet.
1. Løsning med ett farget felt
Når ett felt skal farges, finnes det tre mulige løsninger hvis vi ikke teller med rotasjonene.
2. Løsninger med to fargede felt
Det er seks ulike mønster med to fargede felt.
3. Løsninger med tre fargede felt
Det er ti ulike løsninger med tre fargede felt.
Følg rekkefølgen av figurene, og prøv å se hvordan det er arbeidet systematisk for å få med alle mulige løsninger og unngå å ta med samme løsning to ganger.
Det er mye mer å utforske med disse mønstrene. Lykke til med kreativ utforskning!
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Oppgaven er en god aktivitet for å visualisere symmetri, og for å oppmuntre elevene til å arbeide systematisk. Det er mye å utforske, mange måter å arbeide med utforskningen på, og gode muligheter for å arbeide med problemet, på både et enkelt og et mer krevende nivå. Til slutt kan også elevarbeidene pynte opp klasseromsveggene.
Mulig tilnærming
Ressurser som kan være nyttige:
- Oppgaven kan skrives ut fra denne kopioriginalen.
- Figurene i begynnelsen av oppgaven finnes i denne PowerPoint-filen.
- Ark med kvadratisk rutenett
- Ark med eller isometrisk rutenett
La arbeidet begynne med at elevene får se de to figurene som står i oppgaveteksten og i denne PowerPoint-filen.
|
|
|
La elevene diskutere de to figurene i par, be dem snakke om hva de merker seg med figurene, og hva som er likt og ulikt. Etterpå deler klassen ideene sine.
Forklar så at utfordringen blir å utforske symmetriske mønstre som kan fargelegges i disse to figurene. La elevene få litt tid til å tenke ut forslag til hva de kan utforske. Samle ideene deres på tavla, og føy til flere forslag hvis det trengs.
La elevene velge hvilke problemer de vil utforske, og del ut kopier med kvadratisk og isometrisk ruteark. Gjør oppmerksom på at når arbeidet er avsluttet (etter en eller flere økter), er det forventet at de kan presentere arbeidet sitt. Presentasjonen skal være slik at de kan overbevise klassen om at de har fått med alle mulige løsninger av det problemet de valgte å arbeide med.
Underveis i arbeidet kan det være mange anledninger til å dele tanker og ideer mellom parene. Spesielt er det fint om elevene kan få ideer til systematiske måter å arbeide på.
Gode veiledningsspørsmål
- Hvilke ulike typer symmetri kan dere finne i de to figurene dere arbeider med?
- Hvis du fargelegger en trekant eller et kvadrat inne i figuren her, hvor ellers må du da fargelegge for å skape symmetri?
- Hvilke symmetrier har et ferdig mønster?
- Hvordan kan du være sikker på at du har funnet alle symmetriske mønstre i problemet du arbeider med?
Mulig utvidelse
Problemet kan utvides til 4 · 4 kvadratisk eller isometrisk (triangulært) rutenett.
Og det kan selvsagt utvides til tre dimensjoner.
Mulig støtte
Oppmuntre elevene til først å begynne med å finne alle mulige symmetrier ved å farge ett felt, deretter to, så tre osv.
Hvis noen synes det er vanskelig å se symmetriene, kan du be dem tegne inn symmetrilinja (-linjene).
Foreslå at elevene nummererer feltene i figuren og noterer tallene for hver løsning. Det kan være til hjelp for å holde oversikten.
Tegn er stor tabell på tavla med disse overskriftene i kolonnen:
- 0 symmetrilinjer, 1 symmetrilinje, 2 symmetrilinjer, 3 symmetrilinjer, flere symmetrilinjer.
- Overskrifter for radene:
- Rotasjonssymmetri av orden 1, Rotasjonssymmetri av orden 2, Rotasjonssymmetri av orden 3, rotasjonssymmetri av høyere orden enn 3.
- Fyll inn «Ikke symmetrisk» i den øverste venstre cellen.
Nå kan elevene lime opp sine ulike løsninger på rett plass i tabellen.
Ressursen er utviklet av NRICH