Læreplankoblet

Prismets sideflater

Stikkord: Areal Volum Prisme

Problem

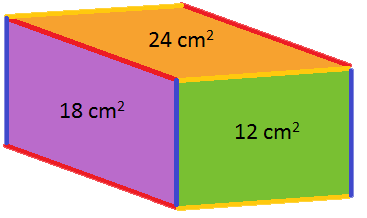
Sideflatene til et rett firkantet prisme har areal 12 cm2, 18 cm2 og 24 cm2.

Hva er prismets volum?

Løsning

Prisme med lilla, grønn og gul flate
Figur 1

Dette bildet viser at:

  • Lengden av den gule sidekanten multiplisert med lengden av den blå sidekanten må bli 12.
  • Lengden av den røde sidekanten multiplisert med lengden av den den blå sidekanten må bli 18.
  • Lengden av den røde sidekanten multiplisert med lengden av den den gule sidekanten må bli 24.

Løsning ved å prøve seg fram

Vi kan begynne med å tenke på to tall som multiplisert med hverandre blir 12. Det vil avgjøre hva den blå og den røde lengden i den lilla flaten må være. Så kan vi kontrollere om vi da får riktig areal på den oransje flaten.

Vi ser på den grønne sideflaten først. Hvis den gule sidekanten er 6 cm, må den blå være 2 cm. Da må den røde sidekanten være 9 cm, siden arealet av den lilla siden er 18 cm2. Den røde lengden multiplisert med den gule lengden blir da 9 cm \(\cdot\) 6 cm = 54 cm2. Denne løsningen går ikke, for vi får feil areal på den siste sideflaten.

Hvis gul lengde er 2 cm, må blå lengde være 6 cm. Da må rød lengde være 3 cm. Det blir feil, for da ville den oransje flaten få areal
2 cm \(\cdot\) 3 cm = 6 cm2.

Hvis gul lengde er 4 cm, blir blå lengde 3 cm. Da blir rød lengde 6 cm. Dette stemmer, for når vi multipliserer gul lengde og rød lengde, får vi nettopp
4 cm \(\cdot\) 6 cm = 24 cm2.

Prismets sidekanter er altså 3 cm, 4 cm og 6 cm lange, og volumet av prismet er da
3 cm \(\cdot\) 4 cm \(\cdot\) 6 cm = 72 cm3.

Å finne sidelengdene ved hjelp av algebra

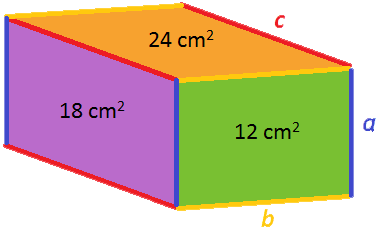
Prisme med lilla, grønn og oransje side
Figur 2

Vi kaller sidelengdene a, b og c. Da er ab =12, ac = 18 og bc = 24.

Herfra kan vi prøve oss fram, slik som ovenfor, eller vi kan bruke ligninger:

\(ab = 12 \implies a = \frac{12}{b}\\ ac = 18\\ \frac{12}{b} \cdot c= 18\\ c=18 \cdot \frac{b}{12} = \frac{3b}{2}\\ bc = 24\\ b \cdot \frac {3b}{2} = 24\\ b^2 = 24 \cdot \frac{2}{3} = 16\\ b=4\\ a= \frac {12}{b}= \frac{12}{4}=3\\ c= \frac{3b}{2} = \frac{3\cdot4}{2} = 6 \)

Vi finner at a = 3 cm, b = 4 cm og c = 6 cm, og volumet av prismet er
3 cm \(\cdot\) 4 cm \(\cdot\) 6 cm = 72 cm3.

Å bruke algebra til å finne volumet direkte

Vi lar sidelengdene være a, b og c som ovenfor.

Volumet av prismet er V = abc.

\(ab \cdot ac \cdot bc=a^2b^2c^2 = (abc)^2 = V^2\\ 12 \cdot 18 \cdot 24 = V^2\\ V = \sqrt{12 \cdot18 \cdot24} = 72\)

Så volumet av prismet er 72 cm3.

Ressursen er utviklet av NRICH

8,9