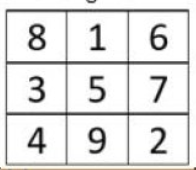
Magisk kvadrat

Hvorfor arbeide med denne oppgaven?

I denne aktiviteten er det magiske kvadratet en kontekst hvor elevene får mulighet til å øve hoderegning, i hovedsak addisjon, og det å arbeide systematisk. Den gir også elevene mulighet til å resonnere over løsninger som ikke fører fram.

Mulig tilnærming

Denne aktiviteten kan introduseres ved at bildet vises for alle elevene.

Be elevene om å tenke individuelt over hvor de kan begynne. Be dem deretter diskutere ideene sine med en partner.  Diskuter til slutt i hele klassen.

Summen av alle sifrene er et nøkkelelement i denne oppgaven, og utfordringen er hvordan denne summen kan brukes for å løse oppaven. Se etter gode strategier som tar utgangspunkt i summen av alle sifrene.

Gode veiledningsspørsmål

Vær litt gnien med veiledningsspørsmålene. La elevene streve før du stiller slike spørsmål!

• Hvordan kan man begynne, og hvorfor?
• På hvilken måte kan du bruke løsningsforslagene som ikke ga riktig løsning i det videre arbeidet?
• Hvordan beholder man en god oversikt over det man har prøvd/funnet ut?
• Hva blir summen dersom vi legger sammen alle tallene?
  • Kan vi bruke denne informasjonen i det videre arbeidet?
  • Hva blir summen i hver rad/kolonne? Hvordan kan denne summen være til hjelp?
  • Hvor mange ulike kombinasjoner gir denne summen?

Mulig utvidelse

Bruk tallene fra 2 til 10 og lag et nytt magisk kvadrat.
Utvid kvadratet til 4x4 ruter og bruk 16 korker.

Mulig støtte

Start med å spørre hva som er totalsummen på melkekorkene til sammen. Deretter kan elevene utfordres til å prøve å finne hvilken sum hver rad/kolonne må ha dersom alle skal ha samme sum.

Hvilke tallkombinasjoner gir sum 15?

Hvilke ruter i 3x3 kvadratet blir “brukt” flest ganger? Hvilke ruter blir “brukt” minst? Ut fra det, hvor er det mest hensiktsmessig å plassere de høyeste og de laveste tallene?Denne informasjonen kan de bruke når de skal legge kvadratet.