Multiplikasjons-aritmagoner
Aktivitet
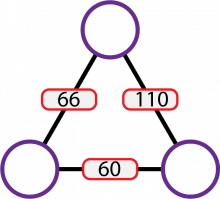
En aritmagon er en polygonEr det samme som en mangekant. En mangekant er en geometrisk lukket figur som er satt sammen av rette linjestykker. Kalles også en polygon. Eksempler på polygon er trekant, firkant, femkant (pentagon) og sekskant (heksagon). med tall i hjørnene og én eller flere regler som bestemmer hvilke tall som skal være på sidene. Vanligvis legger vi sammen tallene i hjørnene for å finne tallene på sidene, men disse aritmagonene følger andre regler. Kan du finne ut hvordan tallene i hjørnene bestemmer tallene på sidene i det interaktive verktøyet under?
Hvis du kjenner verdien av tallene på sidene (i de røde boksene), kan du lage en regel som gjør at du kan finne ut hvilke tall som skal stå i hjørnene?
Bruk det interaktive verktøyet under, og test strategien din.
Det er tre nivåer med ulik vanskelighetsgrad. Begynn med nivå 1.
Når du føler deg trygg på at du kan finne ut hvilke tall som skal stå i hjørnene eller sidene, kan du svare på følgende spørsmål:
- Kan du formulere en regel som gjør at du kan finne ut hva produktene blir på sidene, uavhengig av tallene i hjørnene?
- Er det en sammenheng mellom produkteneProdukt er resultatet av en multiplikasjon, altså det man får når man ganger sammen to eller flere tall eller matematiske uttrykk. i hjørnene og produktene på sidene?
- Hva skjer med tallene i hjørnene hvis du dobler (tredobler, firedobler …) ett eller flere av tallene på sidene?
- Kan du lage en multiplikasjons-aritmagon med ett eller flere tall skrevet som brøk i hjørnene og hele tall skrevet på sidene?
Starthjelp
- Hvilken sammenheng er det mellom produktene på sidene og produktet av tallene i hjørnene?
- Det kan lønne seg å sette navn på tallene i hjørnene, for eksempel A, B og C, og uttrykke sidene ved hjelp av dem.
-
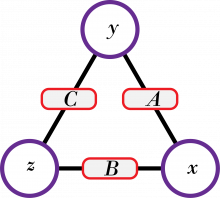
Kall tallene i hjørnene x, y og z, og produktene på sidene A, B og C. Hva er sammenhengen mellom \(A\cdot B \cdot C\) og \(x\cdot y \cdot z\)? Hvordan kan du bruke denne sammenhengen til å bestemme verdiene til x, y og z og når du kjenner verdiene til A, B og C?
Løsning
Tallene på sidene er produktet av tallene i hjørnene. Hvis vi tar produktet av et tall to ganger og finner kvadratrota av tallet, kommer vi tilbake til utgangspunktet. Det samme vil også skje her. Tar vi produktet av tallene på sidene, har vi tatt produktet av tallene i hjørnene to ganger. Kvadratrota vil derfor gi oss produktet av tallene i hjørnene.
Ettersom vi nå har produktet av tallene i hjørnene, kan vi finne hvert enkelt tall ved å dividere produktet med tallene på sidene, fordi tallene på sidene er produktet av tallene i hjørnene.
Eksempel:
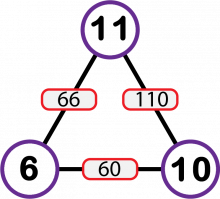
\(\begin{align}66\cdot110\cdot60&=435\:600\\ \sqrt{435\:600}&=\pm 660\\ \\ 660:66&=10 & (-660):66&=-10\\ 660:110&=6 \qquad\lor &(-660):110&=-6\\ 660:60&=11 &(-660):60&=-11\end{align}\)
Vi kan se på dette generelt ved å la x, y og z være hjørnene og A, B og C være sidene. A, B og C er produkt av xy, xz og yz.
Når \(A=xy,\:B=xz\:og\:C=yz\:\:\:\Rightarrow\:\:\:y=\frac Ax\land\:z=\frac Bx\)
Vi kan dermed løse ligningen med hensyn på x:
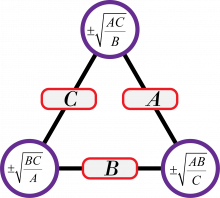
\(\begin{align} yz&=\frac{AB}{x^2}\\ x^2yz&=AB\\ Cx^2&=AB\\ x^2&=\frac{AB}C\\ x&=\pm\sqrt{\frac{AB}C} \end{align}\)
Vi gjør det samme med hensyn på y og z:
\(y=\pm\sqrt{\frac{AC}B}\:\:\:\:\land\:\:\:\: z=\pm\sqrt{\frac{BC}A}\)
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne aktiviteten gir elevene mulighet til å utforske numeriske relasjoner algebraisk. Videre kan de arbeide med å generalisere løsningsstrategiene sine og deretter teste om de stemmer.
Mulig tilnærming
Dersom elevene har tilgang til PC eller nettbrett, kan de bruke det interaktive verktøyet til å utforske multiplikasjons-aritmagoner og finne ut hvilken sammenheng det er mellom tallene på sidene og tallene som skal stå i hjørnene.
Alternativt kan elevene lage sine egne multiplikasjons-aritmagoner. Så kan de gi partneren tallene som skal stå på sidene, og se om han eller hun kan finne ut hvilke tall som skal stå i hjørnene. Begynn med tall fra 1 til 12, utvid deretter til 20–100, og utfordre elevene til å lage multiplikasjons-aritmagoner med brøk eller desimaltall.
Når elevene har fått god tid til å løse flere multiplikasjons-aritmagoner, kan de samles for å dele strategiene de brukte.
Spør deretter: «Kan dere se en sammenheng mellom produktet av de tre tallene på sidene og produktet av tallene i hjørnene?» Hvis elevene ikke har tenkt på denne problemstillingen, bør de få noen minutter til å se på noen eksempler. Oppfordre dem til å bruke algebra til å beskrive den generelle sammenhengen de legger merke til.
Når elevene har utviklet en effektiv metode som fungerer for alle multiplikasjons-aritmagoner, kan de samles for å teste ut metodene på vanskelige multiplikasjons-aritmagoner som de har brukt lang tid på å løse tidligere. Det er for å se hvor kraftfull en generell regel kan være.
Til slutt kan elevene reflektere over disse spørsmålene på bakgrunn av det de har lært om algebraisk tenking og generalisering:
- Hvilke kriterier må ligge til grunn for tallene på sidene for at tallene i hjørnene skal være hele tall?
- Hva skjer med tallene i hjørnene hvis du dobler (tredobler, firedobler …) ett eller flere av tallene på sidene?
- Kan du lage en multiplikasjons-aritmagon med ett eller flere tall skrevet som brøk i hjørnene og hele tall skrevet på sidene?
Gode veiledningsspørsmål
- Er det alltid mulig å finne tallene som er i hjørnene, uansett hvilke tall som er på sidene?
- Hva er sammenhengen mellom produktet av tallene på sidene og produktet av tallene i hjørnene?
Mulig utvidelse
- Kan du lage multiplikasjons-aritmagon der tallene i hjørnene er irrasjonale, samtidig som tallene på sidene er rasjonale?
- Kan du lage multiplikasjons-aritmagon der bare ett eller to av tallene i hjørnene er irrasjonale, samtidig som tallene på sidene er rasjonale?
Ressursen er utviklet av NRICH