GMT
Aktivitet
En variabel X er fordelt på intervallet \( \left\{ x: 0\leq x \leq 3 \right\}\) med følgende sannsynlighetsfordeling:
\(\rho (x) = {2 \over 27} (6+x-x^2)\)
Finn gjennomsnittsverdien, medianen og typetallet til fordelingen.
Starthjelp
Funksjonen ρ beskriver sannsynlighetsfordelingen til en stokastisk variabel X. Ved hjelp av funksjonen kan vi beregne sannsynligheten for ulike utfall \(x\in X\).
Sannsynlighetsfordelingen til en kontinuerlig variabel beskrives med en kontinuerlig funksjon. Vi finner sannsynligheter uttrykt ved arealer under grafen. Da må funksjonen oppfylle kravet
\(\rho(x)\ge 0\quad \text{for}\quad 0\le x\le3\quad \text{og}\quad\int_0^3 \rho(x) dx = 1\).
Vi kan ikke beregne sannsynligheten for ett enkelt utfall i en kontinuerlig sannsynlighetsfordeling, men sannsynligheten for at et utfall som ligger i intervallet mellom a og b, er gitt ved
\(\int_a^b \rho(x) dx = 1\).
Gjennomsnittsverdien er lik forventningsverdien til funksjonen:
\(\mu=\int_0^3 x \cdot \rho(x) dx\).
Medianen er den verdien \(x_m \in X\) som ligger «midt i» fordelingen, det vil si at
\(\int_0^{x_m} \rho(x) dx = \int_{x_m}^3 \rho(x) dx\).
Typetallet (også kalt modus) til fordelingen er den verdien x som har størst frekvens. I en diskret sannsynlighetsfordeling er typetallet den observasjonen som forekommer flest ganger. I en kontinuerlig fordeling svarer det til punktet (x-verdien) der funksjonen har sin maksimumsverdi.
Løsning
Gjennomsnittet eller forventningsverdien finner vi ved formelen
\(\int_0^3 x \cdot \rho(x) dx=\\ \frac2{27}\int_0^3 x \cdot (6+x-x^2) dx=\\ \frac2{27}\int_0^3 (6x+x^2-x^3) dx=\\ \frac2{27}[3x^2+\frac13 x^3 - \frac14 x^4]_0^3=\\ \frac2{27}(27+9-\frac{81}4)=\\ 2+\frac23-\frac64=\\ \frac76\)
Medianen er
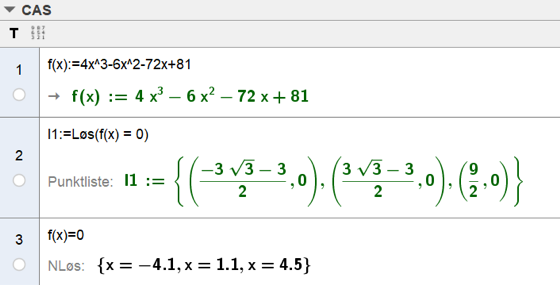
\(\int_0^{x_m}=\frac12\\ \frac2{27} \int_0^{x_m}(6+x-x^2)dx=\frac12\\ \frac2{27}[6x+\frac12 x^2-\frac13x^3]_0^{x_m}=\frac12\\ \frac49 x_m+\frac1{27}x_m^2-\frac 2{81}x_m^3=\frac12\\ 4x_m^3-6x_m^2-72x_m+81=0\)
Vi bruker CAS og finner løsningene:
Av disse løsningene ligger bare \( x=\frac{3\sqrt{3}-3}2\approx1,1\) innenfor definisjonsområdet, så denne x-verdien er medianen.
Funksjonen er en andregradsfunksjon. Fortegnet foran andregradsleddet i funksjonen er negativt, så vi vet at den har en maksimalverdi. Typetallet kan vi finne for eksempel ved hjelp av symmetrilinja til funksjonen:
\(x_{sym}=\frac{-1}{2\cdot(-1)}=\frac12 \).
Dette er typetallet (modus).
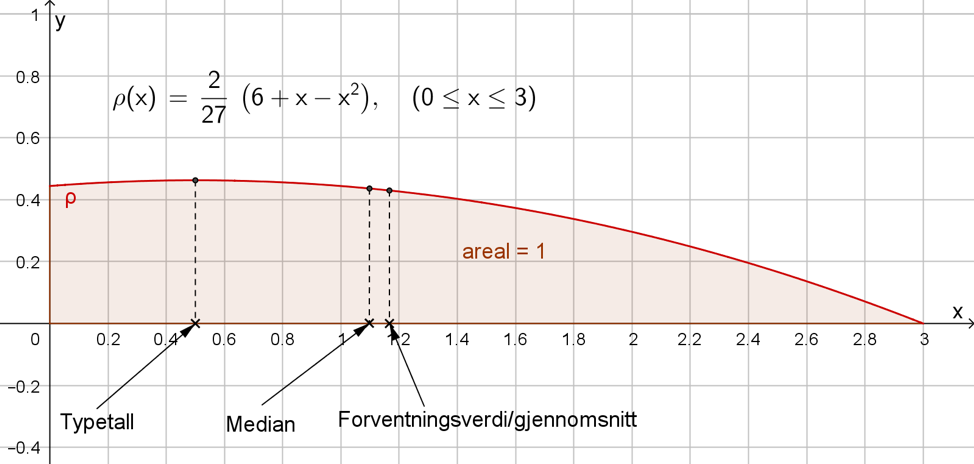
Vi kan tegne grafen til ρ og se hvor disse punktene er plassert:
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Her møter elevene en kontinuerlig sannsynlighetsfordeling som ikke er en normalfordelingsfunksjon. Fordelen med en kontinuerlig funksjon er at vi i stedet for å regne med enkeltverdier kan bruke regneferdigheter som elevene har lært i funksjonslæren.
Mulig tilnærming
Elevene må ha hatt om kontinuerlige sannsynlighetsfordelinger før de får denne oppgaven. Kanskje har de arbeidet med normalfordelingsfunksjonen, og da er ofte kunnskapen om kontinuerlige fordelingsfunksjoner knyttet til akkurat denne funksjonen.
Kan elevene komme på eksempler der de må bruke kontinuerlige fordelingsfunksjoner? Kan de komme på noen som de tror ikke er normalfordelte? For eksempel kan høyden til norske rekrutter, eller vekten på nyfødte kalver til en bestemt kurase, beskrives med en kontinuerlig fordelingsfunksjon. Er disse eksemplene normalfordelt? Hva med levetiden til en viss type lyspærer? Vi kan bruke en kontinuerlig funksjon, men vil den være normalfordelt?
Det er sikkert også nødvendig å snakke om de tre begrepene gjennomsnitt, median og typetall. Under starthjelp står forklaring på begrepene. Kanskje har elevene bare arbeidet med gjennomsnitt og lært at gjennomsnittet i et stort utvalg nærmer seg forventningsverdien, og de har lært formelen for å beregne forventningsverdien.
Men hva skal median og typetall bety i en kontinuerlig fordeling? Diskuter og sammenlign med hva disse begrepene betyr i diskrete fordelinger.
Gode veiledningsspørsmål
- Hva kan du finne ut ved å tegne grafen, for eksempel i GeoGebra?
- Hvor stort er arealet under grafen i definisjonsområdet? Hvorfor blir det slik?
- Hvorfor kan vi si at medianen skal dele arealet under grafen i to?
- Hvorfor sier vi at typetallet er der grafen har sin høyeste verdi?
Ressursen er utviklet av NRICH