Hvor mange baller er det i kurven?
Aktivitet
I en kurv er det noen røde og blå baller. To tilfeldige baller trekkes opp av kurven.
Du får følgende opplysninger:
- Sannsynligheten for å trekke to røde baller er 5 ganger så stor som sannsynligheten for å trekke to blå baller.
- Sannsynligheten for å trekke en ball av hver farge er 6 ganger så stor som sannsynligheten for å trekke to blå baller.
Hvor mange blå og hvor mange røde baller er det i kurven?
Starthjelp
- Hvilke størrelser er ukjente?
- Velg en bokstav for hver av de ukjente.
- Uttrykk sannsynligheten for å trekke 2 blå, 2 røde og 1 ball av hver farge ved hjelp av bokstavene for de ukjente.
- Kan du sette opp en likning for hver av de to opplysningene i oppgaven?
- Kan du løse likningssettet?
Løsning
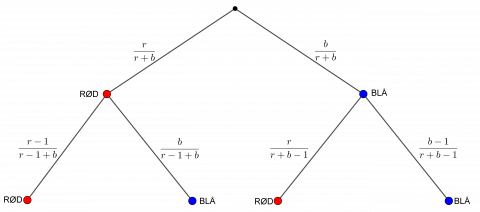
Det kan være en hjelp å tegne et valgtre og skrive sannsynligheten på greinene.
Vi lar r stå for antall røde kuler og b for antall blå kuler.
Sannsynligheten for å trekke to røde baller er \(\frac{r(r-1)}{(r+b)(r+b-1)}\).
Sannsynligheten for å trekke to blå baller er \(\frac{b(b-1)}{(r+b)(r+b-1)}\).
Sannsynligheten for å trekke en ball av hver farge er \(\frac{rb}{(r+b)(r+b-1)}+\frac{br}{(r+b)(r+b-1)}=\frac{2rb}{(r+b)(r+b-1)}\).
Brøkenes nevner kan ikke bli 0, og det blir de ikke hvis \(r\geq 0\) og \(b\geq 0\).
Vi får to likninger:
\(\frac{r(r-1)}{(r+b)(r+b-1)}=5 \frac{b(b-1)}{(r+b)(r+b-1)}\qquad|\qquad\cdot(r+b)(r+b-1)\)
\(r(r-1)=5b(b-1)\qquad\qquad(1)\)
\(\frac{rb}{(r+b)(r+b-1)}+\frac{br}{(r+b)(r+b-1)}=\frac{2rb}{(r+b)(r+b-1)}\\ \frac{2rb}{(r+b)(r+b-1)}=\frac{6b(b-1)}{8r+b)(r+b-1)}\qquad|\qquad\cdot(r+b)(r+b-1) \)
\(2rb=6b(b-1)\qquad\qquad(2)\)
Likning (2) gir
\(r=3(b-1)\\ r=3b-3 \)
Vi setter dette uttrykket for r inn i (1):
\(\begin{align}(3b-3)( 3b-3-1)&=5b(b-1)\\ b^2-4b+3&=0\\ b=1 \:\text{og}\:b&=3 \end{align}\)
Hvis b = 1, er \(r=3\cdot1-3=0\).
Men siden \(r\neq0,\:\text{så må}\: b\neq1\).
Vi forkaster derfor løsningen b = 1.
\(b=3\implies r=3\cdot3-3=6\)
Det er 6 røde baller og 3 blå baller i kurven.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Oppgaven gir øving i å oversette verbal informasjon til uttrykk for sannsynligheter. Deretter må elevene bruke informasjonen de får, til å sette opp likninger og løse dem.
Gode veiledningsspørsmål
- Hvilke størrelser er ukjente?
- Hva er sannsynligheten for utfallene som oppgaven nevner?
- Kan du sette opp likninger der du bruker sannsynlighetene du har funnet?
Mulig støtte
Elevene kan gjerne sette opp uttrykk for sannsynlighetene direkte, men hvis noen synes det er vanskelig, kan det være en hjelp å tegne et valgtre og skrive på sannsynlighetene, slik det er vist under «Løsning».
En annen måte er å begynne med et valgt eksempel, for eksempel 4 blå og 7 røde kuler. Hvor store blir sannsynlighetene for de tre utfallene da? Be elevene skrive opp uttrykkene for sannsynlighetene. La dem deretter bytte ut 4 og 7 i regnestykkene med bokstavene for antall blå og røde baller, r og b, og uttrykke sannsynligheten med disse bokstavene.
Ressursen er utviklet av NRICH