Et litt rundt “kvadrat”
Aktivitet
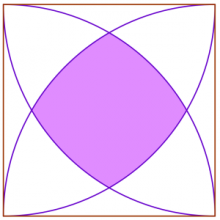
I et kvadrat med sidelengde 1 er det tegnet inn buer med radius 1 med sentrum i hvert hjørne, slik figuren viser. Buene skjærer hverandre inne i kvadratet i fire punkter som blir hjørnene i det fargede området.
Hvor stort er arealet av det største kvadratet som det er mulig å tegne inne i det fargede området?
Er dette en god tilnærming til arealet av det fargede området?
Regn ut hvor stort det fargede arealet er
Hvordan forholder dette seg til tilnærmingen du regnet ut først (kvadratet)?
Kan du finne mer enn én måte å regne ut det fargede arealet på?
Starthjelp
- Du kan løse dette problemet ved å bruke de grunnleggende egenskapene til en sirkel, du kan bruke koordinatgeometriKoordinatgeometri er en gren av geometri der geometriske figurer og objekt blir beskrevet ved hjelp av koordinater og der metoder fra algebra og matematisk analyse anvendes for å løse problemer. og Pytagoras’ setning, eller du kan bruke enkel trigonometri.
For å finne arealet av det største kvadratet inne i det fargede området
- Tenk deg det store kvadratet plassert i et koordinatsystem med origo i nedre venstre hjørne. Hva blir koordinatene til hjørnene i kvadratet?
- Kan du finne lengden av sidene eller diagonalene?
For å finne arealet av det fargede området:
Løsning
Areal av størst mulig kvadrat inne i det fargede området:
Vi tenker oss det store kvadratet plassert i et koordinatsystem, slik figuren viser. Likningen til sirkelen gjennom P og R er \(x^2+y^2=1\). I punktet P er \(x=\frac12\) og vi setter denne x-verdien inn i likningen:
\((\frac12)^2+y^2=1\\ y=\pm \sqrt{1-\frac14}\\ y=\frac{\sqrt 3}{2}\)
Vi velger den positive verdien fordi halvsirkelen ligger over x–aksen.
Vi bruker symmetrien om linja y = x og finner at koordinatene til punktene P og R er \(P(\frac12, \frac{\sqrt3}{2})\) og \(R(\frac{\sqrt3}{2},\frac12)\).
Vi kan bruke Pytagoras’ setning og finne PR, som er sidelengden i det største kvadratet inne i det fargede området:
\(PQ=QR=\frac{\sqrt3}{2}-\frac12\\ PR=\sqrt{2(\frac{\sqrt3}{2}-\frac12)^2}=\frac{\sqrt3-1}{\sqrt2}\)
Arealet av kvadratet med sidelengde PR blir
\(PR^2=(\frac{\sqrt3-1}{\sqrt2})^2=\frac{4-2\sqrt3}{2}=2-\sqrt3.\)
Areal av det fargede området, løsningsalternativ 1:
Vi kan finne vinkelen POR for eksempel ved vektorregning:
\(\vec {OP}\cdot\vec{OR}=|\vec {OP}||\vec{OR}|\cos \angle POR\\ \angle POR= [\frac12, \frac{\sqrt3}{2}]\cdot[ \frac{\sqrt3}{2},\frac12]=\frac{\sqrt3}{2}\\ \angle POR= \frac{\pi}{6}\)
Det vil si at arealet av sektoren POR er \(\frac{1}{12}\) av sirkelarealet \(\pi \cdot 1^2\). Sektorens areal er \(\frac{\pi}{12}\).
Trekantene POQ og ROQ er kongruente og har areal
\(\frac12(\frac{\sqrt3}{2}-\frac12)\cdot\frac12=\frac{\sqrt3-1}{8}.\)
Arealet av den buede figuren PQR = \(\frac{\pi}{12}-2\cdot\frac{\sqrt3-1}{8}=\frac{\pi}{12}-\frac{\sqrt3-1}{4}\), og det fargede arealet består av fire slike kongruente figurer. Så arealet av det fargede området blir
\(4\cdot(\frac{\pi}{12}-\frac{\sqrt3-1}{4})=\frac{\pi}{3}-\sqrt3+1\).
Areal av det fargede området, løsningsalternativ 2:
Vi kan også integrere sirkelbuen gjennom P og R mellom P og R for å finne arealet over x-aksen og under denne delen av buen.
Vi må integrere \(y=\sqrt{1-x^2}\) mellom \(x=\frac12 og x=\frac{\sqrt3}{2}\).
Vi substituerer \(x=\cos t\) som gir \(\frac{dx}{dt}=-\sin t\:\implies dx=-\sin tdt\) og \(y=\sqrt{1-(\cos t)^2}=\sqrt{(\sin t)^2}=\sin t\).
De nye grensene for integrasjon:
\(x=\frac12 \: \implies \: \sin t = \frac12 \: \implies \: t=\frac{\pi}{3}\\ x=\frac{\sqrt3}{2} \: \implies \sin t = \frac{\sqrt3}{2} \: \implies \: t=\frac{\pi}{6}\)
\(\int\limits_{\frac12}^ {\frac {\sqrt3}{2}} \sqrt{1-x^2}dx=\\ -\int\limits_{\frac{\pi}{3}}^{\frac{\pi}{6}} (\sin t)^2 dt=\\ \int\limits_{\frac{\pi}{6}}^{\frac{\pi}{3}} \frac12(1-\cos(2t))dt=\\ \bigg[\frac12 t -\frac14 \sin(2t)\bigg] _{\frac{\pi}{^6}}^{\frac{\pi}{3}} =\\ \bigg(\frac{\pi}{6} -\frac{\sqrt3}{8} \bigg) - \bigg(\frac{\pi}{12} - \frac{\sqrt3}{8} \bigg)=\\ \frac{\pi}{12}\)
Vi må trekke ifra arealet av et rektangel med sidelengder \(\frac{\sqrt3 -1}{2} og \frac12\), arealet av rektangelet blir \(\frac{\sqrt3 -1}{4}\).
Arealet av den buede «trekanten» PQR blir \(\frac{\pi}{12}-\frac{\sqrt3-1}{4}\) og det fargede arealet er fire ganger så stort: \(\frac{\pi}{3}-\sqrt3+1\).
Vi sammenligner de to arealene:
Areal av det fargede området – arealet av det største innskrevne kvadratet = \(\frac{\pi}{3}-\sqrt3+1 - 2 + \sqrt 3=\frac{\pi}{3}-1\approx 0,0472\).
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette problemet kobler sammen mange sider av kunnskap om geometri: koordinatgeometri, sirkellikninger, vektorregning, trigonometri, og om en vil, integralregning.
Mulig tilnærming
Begynn med å vise fra figuren som oppgaven tar utgangspunkt i. Figurene du trenger å vise, finnes også i denne PowerPoint-filen. (PP)
Gi elevene tid til å studere figuren og notere seg alle opplysninger de vet eller kan finne ut. Gi dem utfordringen med å finne det fargede arealet. Etter en stund kan de i fellesskap dele ideer til mulige strategier.
Støtte til å regne med to mulige strategier finnes på arbeidsark:
Å finne areal av sektor og trekanter.
Å finne areal ved å integrere.
Du kan skissere gangen i de to ulike metodene og gi elevene tid til å løse problemet på egen hånd, men tilby arbeidsark til dem som sitter helt fast.
Sett av tid til å la elevene dele og sammenligne ulike tilnærminger og løsninger.
Gode veiledningsspørsmål
- Hvilken informasjon trenger du for å finne arealet?
- Hvilke symmetrier finner du i figuren? Ser du noen linjer som deler figuren opp på en måte som kan gi deg hjelp i utregningen?
- Hvilken av buene i figuren vil det være enklest å arbeide med? Hvorfor?
- Hvordan kan en bruke integrasjon for å finne arealet?
Mulig utvidelse
- Å finne arealet av andre deler av figuren.
- Å lage et lignende problem, men med parabler i stedet for sirkler.
Mulig støtte
Kopioriginalene setter figuren inn i et koordinatsystem og gir veiledning som elevene kan følge.
Ressursen er utviklet av NRICH