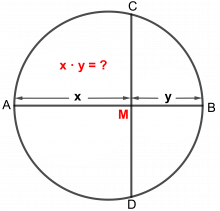Sirkeltrening
Aktivitet
Her kommer tre problemer som alle handler om sirkler.
Prøv å løse dem!
Kan du finne sammenhenger mellom de tre problemene?
Første problem
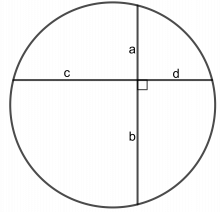
Vis at ab = cd (a, b, c og d representerer lengder).
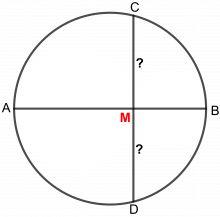
Andre problem
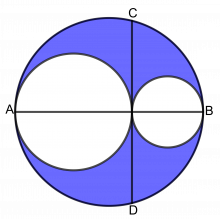
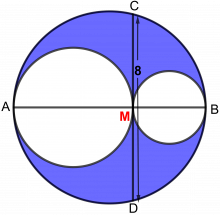
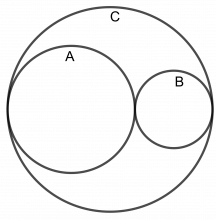
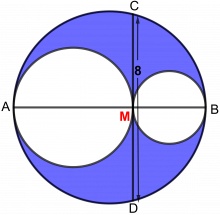
Disse tre sirklene er tegnet slik at de tangerer hverandre, og alle tre har sentrum på linja AB.
Hvis CD = 8, hva er da arealet av det fargede området?
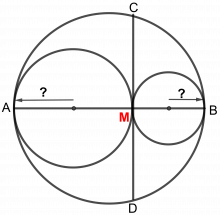
Tredje problem
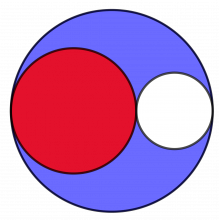
Hvis det blåfargede arealet er like stort som arealet av den største innskrevne sirkelen (rød), hva er da forholdet mellom radiene i de tre sirklene?
Starthjelp
Første problem
|
|
|
|
|
|
\(\frac{b}{c}=\frac{?}{?}\\ \frac{b}{d}=\frac{?}{?}\)
Andre problem
|
|
|
|
|
|
Radien i sirkelen på AM = ? Arealet av sirkelen på AM = ?
Radien i sirkelen på MB = ? Arealet av sirkelen på MB = ?
Radien i sirkelen på AB = ? Arealet av sirkelen på AB = ?
Tredje problem
|
|
|
Radien i sirkel A = x
Radien i sirkel B = y
Radien i sirkel C = ?
Areal A = areal C – areal A – areal B
Løsning
Første problem
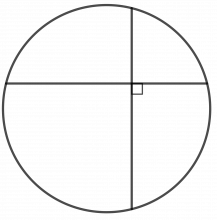
Vi tegner to hjelpelinjer slik at vi får to trekanter. To og to vinkler i trekantene er like store fordi de er periferivinkler som spenner over samme bue. Da har vi to formlike, rettvinklede trekanter.
Ved formlikhet får vi
\(\frac{b}{c}=\frac{d}{a}\\ ab=cd \)
Andre problem
La radien i den største hvite sirkelen være R og i den minste hvite sirkelen r. Da er radien i den store blå sirkelen R + r.
Blått areal = \(\pi(R+r)^2-\pi R^2-\pi r^2= \pi(R^2+2Rr+r^2-R^2-r^2)=2\pi Rr\)
Vi ser at CM = MD = 4, siden AB er diameter i sirkelen. Vi bruker regelen vi fant i første problem:
\(AM\cdot MB= CM\cdot MD\\ 2R\cdot 2r=4\cdot 4\\ Rr=4\)
Arealet av det blå området er
\(2\pi Rr=2\pi 4=8\pi\)
Tredje problem
Vi lar fortsatt radien i den største hvite sirkelen være R og i den minste hvite sirkelen r. Vi bruker også formelen for det blå arealet som vi fant ovenfor. Hvis det blå området er lik arealet av den største innskrevne sirkelen, må
\(\pi R^2=2\pi Rr\\ R=2r\)
Da vil radien i den store sirkelen være \(R+r=2r+r=3r\), og forholdet mellom radiene i de tre sirklene er
1 : 2 : 3.
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Dette problemet kobler sammen viktige ideer om formlike trekanter, egenskaper til linjer i en sirkel og en del algebra. Det er et eksempel på at problemer kan løses selv om det tilsynelatende er gitt begrenset med informasjon. Problemene kan brukes til å øve på å forstå andres argumenter og forklaringer. Hensikten med å samle tre problemer er å oppmuntre til diskusjon om sammenhengen mellom dem, og gi elevene erfaringer med hvordan en i problemløsning kan utnytte egenskaper og sammenhenger en tidligere har funnet.
Mulig tilnærming
Oppgaven kan skrives ut fra en kopioriginal her.
Hensikten med det første problemet er å få elevene til å se nytten av hjelpelinjer, og at det i dette tilfellet kan gi formlike trekanter.
Begynn med å dele ut oppgaven og gi elevene god tid til å reflektere og diskutere. Hvis det ikke kommer noen ideer til hva en kan prøve på, kan du vise dem figuren med de to hjelpelinjene inntegnet. Kanskje er det tilstrekkelig å vise figuren, og så får elevene en ny sjanse til å se gangen videre selv. Eller du kan spørre:
«Vi har fått to trekanter. Har disse trekantene noe til felles? I tilfelle hva?»
«Hva vet vi om vinklene i de to trekantene?»
- De er rettvinklet.
- To og to vinkler er like store. Hvorfor?
- Trekantene er formlike.
Få alle med på å se hvordan en får resultatet ab = cd ved å bruke formlikhet. Lag noen eksempler, som: «Hvis a = 3, b = 5, c = 6, hva må da d være?»
I arbeidet med de neste to problemene kan «Starthjelp» være nyttig. Du kan skrive ut starthjelpen til de tre problemene her.
Denne starthjelpen er ganske omfattende. Å studere den kan gi elevene god øving i å bruke en matematisk tekst til å se flere sammenhenger, få nye ideer og komme til et punkt der de selv kan oppdage en løsning.
Når elevene har forstått løsningen på alle de tre problemene, er det tid for i fellesskap å se på sammenhengen mellom disse tre – hva som er likt, hva som er forskjellig, og hva det er viktig å merke seg.
I periodene når elevene arbeider på egen hånd (gjerne i par), er det nyttig å la dem streve og bruke litt tid. I stedet for å veilede dem til raskt å finne løsninger kan læreren observere og prøve å merke seg de gangene elever får en idé som fører dem videre. Hva var det som gjorde at en ny tanke dukket opp? Brukte elevene kunnskaper og erfaringer fra tidligere? Hvilken kunnskap? Eller kom de på å prøve noe som var nytt for dem? Var det i diskusjonen at nye ideer oppstod?
Gode veiledningsspørsmål
- Hvilke hjelpelinjer kan du tegne inn for å få flere egenskaper tydeligere fram?
- Finner du noen formlike trekanter?
- Hvorfor trenger du ikke bekymre deg om π?
- Hva har de to første problemene til felles?
- Hva har de to siste problemene til felles?
- Kan du komme på andre problemer der du bruker noen av de samme ideene?
Ressursen er utviklet av NRICH