Heltall på ei kule
Problem
En kule med radius 3 har sentrum i origo.
Hvor mange punkter på kulens overflate har koordinater der alle tre er hele tall?
Løsning
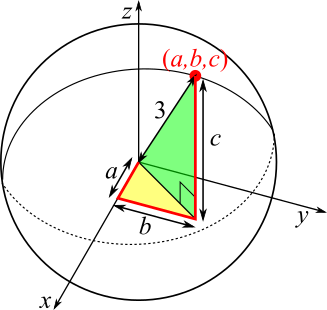
Vi tenker oss kula plassert i koordinatsystemet og et punkt (a, b, c) på kuleoverflaten, slik figuren viser.
Både den gule og den grønne trekanten er rettvinklet. Hypotenusen i den gule trekanten er katet i den grønne trekanten, og denne siden kaller vi k. Hypotenusen i den grønne trekanten er radien i kula, den har lengde 3.
I den gule trekanten er a2 + b2 = k2.
I den grønne trekanten er k2 + c2 = 32 → a2 + b2 + c2 = 9
Siden a, b og c skal være hele tall som ikke er større enn 3, må a2, b2 og c2 være enten 0, 1, 4 eller 9.
Vi kan lete etter mulige løsninger ved å velge en verdi for a2 først og så en verdi for b2 som er slik at
a2 + b2 ≤ 9. Til slutt finner vi den verdien for c2 som gjør a2 + b2 + c2 = 9.
|
a2 |
b2 |
c2 |
(a, b, c) |
|
0 |
0 1 4 9 |
9 8 (umulig) 5 (umulig) 0 |
(0, 0, 3), (0, 0, -3)
(0, 3, 0), (0, -3, 0) |
|
1 |
0 1 4 |
8 (umulig) 7 (umulig) 4 |
(1, 2, 2), (1, 2, -2), (1, -2, 2), (1, -2, -2) (-1, 2, 2), (-1, 2, -2), (-1, -2, 2), (-1, -2, -2) |
|
4 |
0 1
4 |
5 (umulig) 4
1 |
(2, 1, 2), (2, 1, -2), (2, -1, 2), (2, -1, -2) (-2, 1, 2), (-2, 1, -2), (-2, -1, 2), (-2, -1, -2)
(2, 2, 1), (2, 2, -1), (2, -2, 1), (2, -2, -1) (-2, 2, 1), (-2, 2, -1), (-2, -2, 1), (-2, -2, -1) |
|
9 |
0 |
0 |
(3, 0, 0), (-3, 0, 0)
|
Dette gir 6 mulige kombinasjoner av a2, b2 og c2. Vi må huske på at ligninger på formen \(x^2=n\), der \(n\) er er et positivt tall, har to løsninger: \(x=\pm\sqrt{n}\).
Det blir i alt 30 punkter på kuleflaten med bare heltallige koordinater.
Ressursen er utviklet av NRICH