Semiregulær tessellering
Aktivitet
Regulære tesselleringer bruker identiske regulære mangekanter til å fylle planet. Mangekantene settes sammen med hjørne mot hjørne og kant mot kant, uten noen gap imellom.
Kan du overbevise deg selv om at det finnes bare tre regulære tesselleringer?
Semiregulære tesselleringer har to egenskaper:
- De er satt sammen av to eller flere typer regulære mangekanter som har samme sidelengde.
- Hvert hjørne har samme mønster av mangekanter rundt seg.
Bruk GeoGebra-appleten nedenfor til å utforske semiregulære tesselleringer.
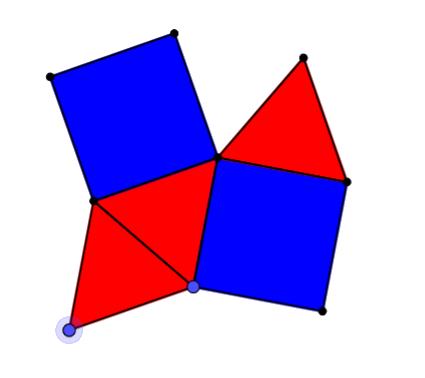
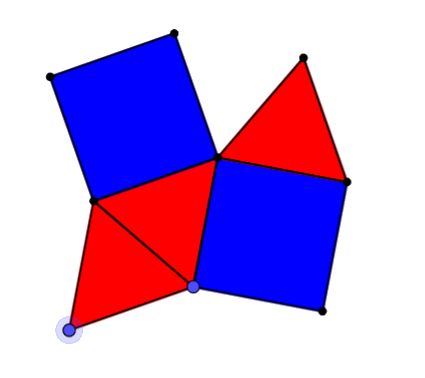
Figuren nedenfor viser en organisering av likesidede trekanter og kvadrater. Det ser ut som det er plass til en trekant til for å tette hullet på toppen. Kan du bevise at en trekant vil fylle hullet?
Om vi legger dette mønsteret i planet kan vi representere det som {3, 4, 3, 3, 4}, fordi vi følger mønsteret «trekant, firkant, trekant, trekant, firkant» rundt hvert punkt. Hvordan ville mønsteret se ut om du endret den rekkefølgen?
Kan du finne alle semiregulære tesselleringer?
Kan du vise at du har funnet alle?
Du kan skrive ut kopioriginalene 3, 4, 5, 6, 8, 9, 10 og 12 om du vil arbeide uten GeoGebra-appleten.
Starthjelp
Her er noen metoder som du kan bruke for å finne vinklene i regulære nikanter:
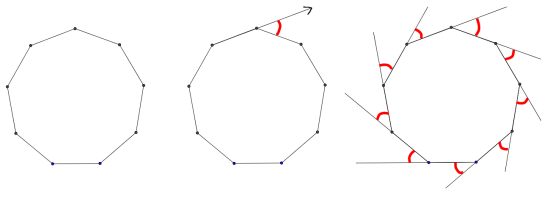
Se for deg at du går rundt en regulær nikantet park.
Den andre figuren viser vinkelen du må svinge når du kommer til det første hjørnet.
Den tredje figuren viser alle vinklene du svinge for å komme rundt hele parken én gang.
Hvor mange grader svinger du til sammen?
Hvor stor må hver vinkel på utsiden være?
Hvor stor må hver vinkel på innsiden være?
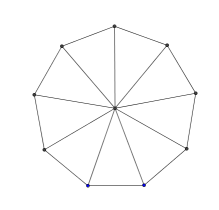
Her ser du en regulær nikant.
Den har blitt delt opp i ni likebeinte trekanter.
Hva er summen av alle vinklene i alle trekantene?
Subtraher vinklene som dannes rundt sentrum, slik at du finner summen av alle vinklene i hjørnene til nikanten.
Hvor stor må hver vinkel i nikanten være?
Kan du tilpasse disse metodene til noen andre regulære mangekanter?
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Tessellering er et tema som elever i alle aldre blir fascinert av. Det virkelighetsnære aspektet ved å legge fliser eller lage vakre mønstre kan være en motiverende faktor for mange. Den interaktive GeoGebra-appleten gir elevene mulighet til å teste ut ideene sine på en rask måte, samtidig som den kan være en støtte for påstander.
For å løse problemet med å finne alle mulige tesselleringer kreves det at elevene arbeider med vinkler i mangekanter og vinkler rundt punkter.
Mulig tilnærming
Introduser det interaktive verktøyet for klassen, og be elevene vurdere hvilke figurer de ville valgt om de skulle flislagt et areal (med bare en type figur), uten at de overlapper hverandre, eller at det blir gap mellom dem. Test ut forslag som elevene kommer med, med GeoGebra-appleten for å se om figurene tessellerer eller ikke.
Be klassen om å tenke på hvorfor noen figurer tessellerer og andre ikke. Om klassen har foreslått bare trekanter, kvadrater og sekskanter så langt, kan du be dem vurdere hva som vil skje med femkanter.
Se Starthjelp for metoder for å beregne vinklene i regulære mangekanter, hvis elevene dine ikke har arbeidet med det tidligere.
Når dere har konkludert med at de innvendige vinklene i mangekanter som tessellerer må være en faktor i 360, kan du utfordre elevene til å utforme overbevisende argumenter for at det finnes bare tre regulære tesselleringer.
Deretter kan du innføre begrepet semiregulær tessellering.
«Hva om du kunne bruke mer enn én type figur til å flislegge området ditt?»
Be elevene om å komme med forslag, eller vis denne figuren:
«Hvilken figur må jeg ha for å tette hullet på toppen? Vil den passe nøyaktig? Hvordan vet dere det?»
Tre likesidete trekanter pluss to kvadrater gir 60˚ + 60˚ + 60˚ + 90˚ + 90˚ = 360˚.
Deretter kan du introdusere notasjonen som beskriver mangekantene rundt hvert hjørne: {3, 4, 3, 3, 4} for eksemplet over.
NB! I semiregulær tessellering må hvert hjørne ha nøyaktig samme figurer rundt seg, i nøyaktig samme rekkefølge (de kan gå med eller mot klokka). Om du for eksempel bruker trekanter og sekskanter og plasserer {3, 6, 6, 3} rundt ett punkt, kan du ikke ha {3, 6, 3, 6} rundt et annet.
Gi elevene utfordringen med å finne semiregulære tesselleringer. Oppfordre dem til å bruke innvendige vinkler til å finne kombinasjoner av figurer som kan tessellere. Når de har kommet med en påstand, kan de teste den ut med GeoGebra-appleten, eller ved hjelp av figurer som er skrevet ut og klipt ut. I lista over kopioriginaler finner du regulære figurer som kan skrives ut.
Det er viktig at elevene prøver med mange figurer for å få bekreftet at tesselleringen fungerer. En tikant og to femkanter passer sammen rundt et punkt, men mønsteret kan ikke gjentas.
Når elevene har fått mulighet til å finne en eller to semiregulære tesselleringer, utfordrer du dem til å finne alle, samtidig som de må sørge for overbevisende argumenter eller bevis for at de har funnet alle.
Gode veiledningsspørsmål
- Hvorfor passer noen figurer sammen og andre ikke?
- Kan du forutse om figurer vil tessellere, uten å bruke det interaktive verktøyet?
- Kan du organisere/systematisere arbeidet ditt på en slik måte at du kan overbevise andre om at du har funnet alle semiregulære tesselleringer?
Mulig utvidelse
Kan elevene forklare hvorfor noen kombinasjoner fungerer rundt et punkt, men ikke kan brukes til å flislegge et areal? Det gjelder for eksempel tikanten og femkantene som nevnt over. Be elevene finne lignende eksempler (der de kan bruke mangekanter med mer enn 12 sider, for eksempel {18, 9, 3}).
Mulig støtte
Elevene kan begynne med å utforske tessellering med firkanter, og ha spesielt fokus på egenskapene til vinklene.
Ressursen er utviklet av NRICH