Steiner på stranda
Aktivitet
Se for deg at du går på ei fin sandstrand, så får du øye på noen små steiner her og der. Du plukker opp fire steiner og legger dem slik at de danner form som et kvadrat. Arealet av kvadratet er 1 kvadrat-ett-eller-annet, kanskje 1 kvadratmeter, 1 kvadratcentimeter, 1 kvadratfinger, 1 kvadratsko, osv.
Vi kan si at kvadratet du har lagt, skal ha areal 1.
Ved å legge til to nye steiner kan vi doble arealet fra 1 til 2, slik:
Regelen som utvikler seg her, er å ikke røre steinene som allerede er lagt, og legge til så få steiner som mulig for å doble det forrige arealet. Det er bare lov å legge rektangler.
Så hvis vi fortsetter, kan vi legge til tre nye steiner for å doble arealet fra 2 til 4, slik:
Her trengte vi tre nye steiner.
Det er også mulig å doble arealet fra 2 til 4 ved å gjøre slik:
Her brukte vi fire steiner. En slik løsning følger ikke regelen om å bruke så få steiner som mulig, så denne løsningen er ikke gyldig.
Nummer 6 vil se slik ut:
Husk! Ikke flytt på steinene som er lagt, og doble det forrige arealet ved å legge til så få steiner som mulig hver gang.
Nå er det din tur!
Se på formene du har laget. Legger du merke til noe spesielt?
Lag noen flere. Hvor mange kan du lage? Du vil kanskje gå tom for tellebrikker, perler eller hva du enn bruker.
Utforsk dette:
- Hvor mange ekstra steiner må du legge til hver gang? Det starter slik: 2, 3, 6 …
- Hvor mange steiner er det rundt den ytterste kanten? Det starter slik: 4, 6, 8 …
- Hvor stort er arealet? Det starter slik: 1, 2, 4 …
- Hvor mange steiner er det inni rektanglene? Det starter slik: 0, 0, 1, 3, 9 …
Kan du finne på noen spørsmål selv?
Spør deg selv: «Hva vil skje hvis ..?»
Forsøk å svare på disse spørsmålene og andre spørsmål du kommer på selv, og noter resultatet i et skjema.
Starthjelp
- Bruk konkreter til hjelp, for eksempel tellebrikker og et ruteark.
- Kan du lage et rektangel med bare én stein til? Hva med to? Tre?
- Har du forsikret deg om at hvert rektangel har dobbelt så stort areal som det forrige?
- Hvordan holder du styr på det du har gjort?
Løsning
|
Nummer |
Form |
Antall steiner |
Areal |
Omkrets |
|
1 |
Kvadrat |
2 · 2 = 4 |
1 cm2 |
4 cm |
|
2 |
Rektangel |
2 · 3 = 6 |
2 cm2 |
6 cm |
|
3 |
Kvadrat |
3 · 3 = 9 |
4 cm2 |
8 cm |
|
4 |
Rektangel |
3 · 5 = 15 |
8 cm2 |
12 cm |
|
5 |
Kvadrat |
5 · 5 = 25 |
16 cm2 |
16 cm |
|
6 |
Rektangel |
5 · 9 = 45 |
32 cm2 |
24 cm |
|
7 |
Kvadrat |
9 · 9 = 81 |
64 cm2 |
32 cm |
|
8 |
Rektangel |
9 · 17 = 153 |
128 cm2 |
48 cm |
Lærerveiledning
Hvorfor arbeide med denne oppgaven?
Denne aktiviteten har en utforskende tilnærming der elevene må forholde seg til både rom og form. I tillegg legger aktiviteten til rette for at elevene kan utvikle tallforståelsen sin. Aktiviteten kan være krevende i den forstand at de ofte må jobbe litt for å komme til svaret. Det gir deg som lærer en fin mulighet til å teste elevenes utholdenhet og utvikle den.
Mulig tilnærming
En fin måte å starte denne aktiviteten på er å samle hele klassen og lage de to eller tre første arealene sammen. Det kan være nyttig for elevene å ha ruteark tilgjengelig, gjerne med uthevede prikker, og små tellebrikker som kan representere steinene. Et interaktivt geobrett kan brukes på smartboard til å vise og til å dele elevenes ideer.
Etter at elevene har arbeidet i par en stund, og undersøkt ulike tallmønster som oppstår, kan du stille noen av spørsmålene under for å invitere elevene til selv å stille og utforske deres egne spørsmål. Oppmuntre dem til å notere og holde styr på oppdagelsene sine på den måten de selv mener er best.
Gode veiledningsspørsmål
-
Hva teller du? (Noen ganger kan det oppstå forvirring når elevene skal telle steiner eller antall mellomrom mellom steinene, spesielt når de skal telle sidene.)
- Har dette rektanglet eller kvadratet dobbelt så stort areal som det forrige?
- Hvordan holder du styr på det du har kommet fram til så langt?
Mulig utvidelse
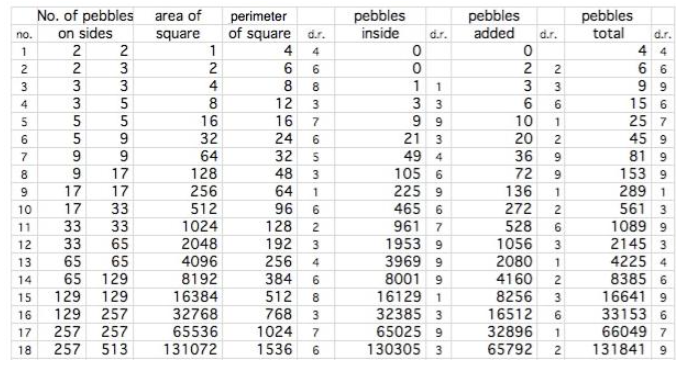
Noen elever velger å holde styr på oppdagelsene sine ved å lage en tabell eller bruke et regneark. Når de noterer resultatene systematisk, har de mulighet til å utforske videre.
Her er et eksempel:
d.r.= digital root (sifferrot).
Eksempel: Sifferroten av 247 = 4, fordi 2 + 4 + 7 = 13 og 1 + 3 = 4)
Send inn elevsvar
Ressursen er utviklet av NRICH